Интегральная форма теоремы об изменении количества движения
Теорему об изменении количества движения можно записать также в интегральной (конечной) форме. Пусть в начале и конце некоторого рассматриваемого интервала времени [$t_{1} ,t_{2} $] количество движения равно соответственно $\overline{Q}_{1} ,\overline{Q}_{2} $. Домножим обе части равенства на $dt$ и проинтегрируем на этом интервале:
Произведение вектора силы на бесконечно малый промежуток времени ее действия $\overline{F}{k} dt$ называется элементарным импульсом силы $\overline{F}{k}$.
Интеграл от элементарного импульса на интервале времени [$t_{1} ,t_{2} $]:
называется импульсом (полным импульсом) силы $\overline{F}_{k} $ на этом интервале. С использованием этого понятия теорема запишется в виде:
и читается так:
изменение количества движения механической системы за некоторый (конечный) промежуток времени равно геометрической сумме импульсов внешних сил за тот же промежуток времени. Теорема в такой форме применяется при изучении удара твердых тел.
Подставим в равенство:
выражающее теорему об изменении количества движения в дифференциальной форме, формулу:
служащую для вычисления количества движения, и расшифруем обозначение $\overline{R^{e} }$. В результате придем к равенству:
в точности совпадающему с математическим выражением теоремы о движении центра масс. Откуда следует, что теоремы об изменении количества движения системы и о движении~центра масс вполне тождественны.
Однако по способу выражения общего объективного содержания эти теоремы настолько отличаются, что считаются вполне самостоятельными теоремами динамики. Каждая из теорем имеет свою преимущественную область применения:
- теорема об изменении количества движения в дифференциальной форме применяется в механике сплошной среды;
- в интегральной форме - в теории удара твердых тел;
- теорема о движении центра масс применяется в динамике твердого тела и системы твердых тел.
Космический корабль двигался с постоянной по величине скоростью $v$. Для изменения направления его полета включается двигатель, выбрасывающий струю газа со скоростью $v_{отн} $ относительно корабля в направлении, перпендикулярном к его траектории. Определить угол $\alpha $, на который повернется вектор скорости корабля, если начальная масса его $m_{0} $, а конечная $m$.
Дано: $v$, $v_{отн} $, $m_{0} $, $m$.
Найти: $\alpha $-?
Решение:
Ускорение корабля по абсолютной величине равно:
$a=\omega ^{2} r=\omega v$, причем $v=const$. Поэтому уравнение движения:
$m\frac{dv}{dt} =v_{отн} \frac{dm}{dt} $ переходит в: $mv\omega dt=-v_{отн} dm$.
Так как $d\alpha =\omega dt$ есть угол поворота за время $dt$, интегрируя наше уравнение, получим:
\[\alpha =\frac{v_{отн} }{v} \ln \frac{m_{0} }{m} .\]Ответ: угол поворота вектора скорости равен: $\alpha =\frac{v_{отн} }{v} \ln \frac{m_{0} }{m} $
Ракета перед стартом имеет массу $m_{0} =250$кг. На какой высоте окажется ракета через $t=20$с после начала работы двигателей? Расход топлива равен $\mu =4$кг/с и скорость истечения газов относительно ракеты $v_{отн} $$=1500$м/с постоянны. Поле тяготения Земли считать однородным.
Дано: $m_{0} =250$кг, $t=20$с, $\mu =4$кг/с, $v_{отн} $$=1500$м/с.
Найти: $H$-?
Решение:
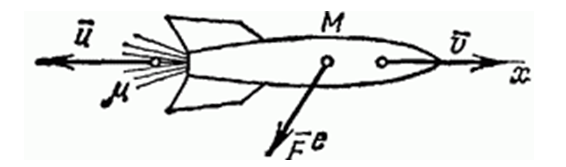
Рисунок 1.
Запишем уравнение Мещерского в однородном поле тяготения Земли в виде:
\[m\frac{\Delta v_{0} }{\Delta t} =\mu v_{отн} -mg,\]где $m=m_{0} -\mu t$, а $v_{0} $- скорость ракеты в момент времени $t$. Разделяя переменные получаем:
\[\Delta v_{0} =(\frac{\mu v_{отн} }{m_{0} -\mu t} -g)\Delta t\]Решение данного уравнения, удовлетворяющего начальному условию $v_{0} =0$при $t=0$, имеет вид:
\[v_{0} =v_{отн} \ln \frac{m_{0} }{m_{0} -\mu t} -gt\]Учитывая что $H_{0} =0$при $t=0$ получим:
\[H=v_{отн} t-\frac{gt^{2} }{2} +\frac{v_{отн} m_{0} }{\mu } (1-\frac{\mu t}{m_{0} } )\ln (1-\frac{\mu t}{m_{0} } ).\]Подставляя начальные значения, получаем:
$H=v_{отн} t-\frac{gt^{2} }{2} +\frac{v_{отн} m_{0} }{\mu } (1-\frac{\mu t}{m_{0} } )\ln (1-\frac{\mu t}{m_{0} } )=3177,5$м
Ответ: через $20c$ ракета окажется на высоте $H=3177,5м. $











