Эквивалентность гравитационных сил силам инерции
Важнейшей особенностью полей тяготения является то, что тяготение совершенно одинаково действует на разные тела, сообщая им одинаковые ускорения, независимо от свойств тел. Это было известно еще в ньютоновской теории и положено в основу новой, эйнштейновской теории тяготения. Под действием гравитационной силы:
все тела на поверхности Земли падают с одинаковым ускорением - ускорением свободного падения. Этот факт был установлен Ньютоном и может быть сформулирован как принцип строгой пропорциональности гравитационной массы $m_{g} $, определяющей взаимодействие тела с полем тяготения, и инертной массы $m_{in} $, определяющей сопротивление тела действующей на него силе и входящей во второй закон Ньютона:
$F=m_{in} a$.
Уравнение движения тела в поле тяготения записывается так:
где $\overline{a}$ - ускорение, приобретаемое телом под действием поля тяготения, напряженностью $\overline{G}=\overline{g}$. В этом случае, согласно Ньютону, для всех тел $m_g=m_{in}$ и $\overline{a}=\overline{g}$ - ускорение не зависит от массы и равно напряженности поля тяготения.
Таким образом, все тела в поле тяготения и в поле сил инерции, при $\overline{a}=\overline{g}$, движутся совершенно одинаково. Например, движение тел в космическом корабле, летящем с ускорением $\overline{a}=\overline{g}$, и в корабле, находящемся на Земле в поле тяжести с напряженностью $\overline{G}=\overline{g}$, будет одинаковым. Силы инерции в ускоренно движущемся корабле будут неотличимы от гравитационных сил, действующих в истинном поле тяготения. Поэтому силы инерции можно считать эквивалентными гравитационным силам.
Тождественность инерциальной и гравитационной масс является следствием эквивалентности сил инерции и сил тяготения. Этот факт называется принципом эквивалентности Эйнштейна.
Принцип относительности Эйнштейна
Исторически принцип относительности был сформулирован Эйнштейном так: все явления в гравитационном поле происходят точно так, же как в соответствующем поле сил инерции, если совпадают напряжённости этих полей и одинаковы начальные условия для тел системы.
Согласно этому принципу, все физические процессы в истинном поле тяготения и в ускоренной системе отсчета, при отсутствии тяготения, протекают одинаковым образом. Это фундаментальный закон природы.
Для доказательства этого принципа Эйнштейн предложил следующий мысленный эксперимент. Пусть тела находятся в лифте, который бесконечно удален от гравитирующих тел и движется с ускорением. Тогда на все тела находящиеся в лифте действует сила инерции, а тела под действием этих сил будут давить на опору или подвес. То есть тела будут обладать весом. Если лифт не движется, а висит над какой-то гравитирующей массой в однородном поле, то все тела также будут обладать весом. Находясь в лифте, невозможно отличить эти две силы. Поэтому все механические явления будут в обоих лифтах происходить одинаково. Эйнштейн обобщил это положение на все физические явления.
Следствием этого закона является то, что, находясь внутри закрытой кабины, невозможно определить, чем вызвана сила $m_g$. Тем, что кабина движется с ускорением или действием притяжения Земли?
Ярчайшим доказательством равенства сил инерции и гравитации является состояние невесомости космонавтов в космическом корабле (падают под действием гравитационных сил и отлетают под действием центробежных сил инерции). Принцип эквивалентности -- основополагающий в ОТО Эйнштейна.
Принципы эквивалентности
Следует различать «слабый принцип эквивалентности» и «сильный принцип эквивалентности».
Сильный принцип эквивалентности можно сформулировать так: в каждой точке пространства-времени в произвольномгравитационном поле можно выбрать «локально-инерциальную систему координат», такую, что в достаточно малой окрестности рассматриваемой точки законы природы будут иметь такую же форму, как и в не ускоренных декартовых системах координат СТО, где под «законами природы» подразумевают все законы природы.
Слабый принцип отличается тем, что слова «законы природы» заменяются в нем словами «законы движения свободно падающих частиц». Слабый принцип - это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип представляет собой обобщение наблюдений за влиянием гравитации налюбые физические объекты.
Часто считают, что принцип эквивалентности является основным принципом общей теории относительности и вообще многих релятивистских теорий гравитации, так как якобы в соответствии с принципом эквивалентности гравитационное поле можно рассматривать как неинерциальную систему отсчёта. Это верно лишь с оговорками. Любая неинерциальная система отсчёта в специальной теории относительности всё равно имеет в основе плоское, неискривлённое пространство-время. В метрических же теориях гравитации, к которым принадлежит иобщая теория относительности, пространство-время искривлено. Неполнота соответствия выявляется тем фактом, что глобальных инерциальных систем отсчёта в метрических теориях просто нет, там все системы - неинерциальные. Даже переход в локально-инерциальную систему отсчёта не удаляет гравитационных эффектов, связанных с кривизной пространства-времени (например, девиацию геодезических или приливные силы). Только если выбирать размеры изучаемой системы намного меньше характерной кривизны, то приблизительно физическими проявлениями искривления можно пренебречь и получить «принцип эквивалентности». В точной же формулировке законов природы кривизна пространства-времени всё равно появляется в некоторых местах, что отличает их от соответствующих законов в специальной теории относительности.
С точки зрения математики во всех метрических теориях гравитации принцип эквивалентности с точностью до оговорок предыдущего пункта тривиально следует из того факта, что в окрестности любого события пространства-времени возможно ввести локально геодезическую систему координат или риманову системукоординат, в которых в заданной точке символы Кристоффеля исчезают, то есть равны $0$. В физикепредпочитают говорить об этом как о существовании локально инерциальных систем отсчёта.
Шарик массы $m$ подвешен внутри пустой цистерны на невесомой нити длиной $l$. В начальный момент времени цистерна начинает двигаться в горизонтальном направлении с постоянным ускорением $a$. Какое движение будет при этом совершать шарик?
Дано: $m, l, а.$
Найти: уравнение движения шарика.
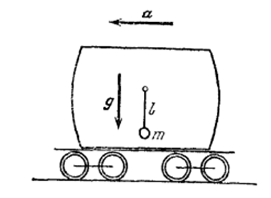
Рисунок 1.
Решение: Вместо того чтобы рассматривать ускоренно движущуюся цистерну, будем считать, что она неподвижна, но на все тела в ней действует дополнительно гравитационное поле $-a=g_{1} $. Это поле, складываясь с истинным полем тяжести Земли, дает эффективное поле тяжести, напряженность которого:
\[g_{2} =g+g_{1} =g-a.\]Вектор $g_{2} $ отклонен от истинной вертикали на угол $\alpha _{0} $, тангенс которого определяется соотношением:
\[tg\alpha _{0} =a/g.\]Напряженность эффективного поля тяжести находится по теореме Пифагора:
\[g_{2} =\sqrt{g^{2} +a^{2} } .\]Ясно, что в положении равновесия нить маятника направлена вдоль вектора $g_{2} $. В начальный момент, когда цистерна начинает двигаться с ускорением $a$ шарик неподвижен, а нить вертикальна, т.е. маятник отклонен от нового положения равновесия на угол $\alpha _{0} $ влево. Поэтому маятник в пустой цистерне будет совершать относительно нового положения равновесия колебания с угловой амплитудой $\alpha _{0} $. Если ускорение цистерны мало по сравнению с ускорением свободного падения, то амплитуда колебаний мала и колебания будут гармоническими. Угол отклонения от нового положения равновесия $\alpha (t)$ будет при этом изменяться со временем по закону:
\[\alpha (t)=-\alpha _{0} \cos \omega t,\]где частота определяется соотношением:
\[\omega =\frac{g_{2} }{l} .\]Ответ: $\alpha (t)=-\alpha _{0} \cos \omega t$.












