
Уравнение движения тела с переменной массой
Под переменной массой будем понимать массу тел, которая при медленном движении тел меняется за счет потери или приобретения вещества.
Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Принцип действия ракеты очень прост. Ракета с большой скоростью выбрасывает вещество (газы), воздействуя на него с большой силой. Выбрасываемое вещество с той же, но противоположно направленной силой в свою очередь действует на ракету и сообщает ей ускорение в противоположном направлении. На ракету действуют внешние силы: сила земной тяжести, гравитационное притяжение Солнца и планет, а также сила сопротивления среды, в которой движется ракета.
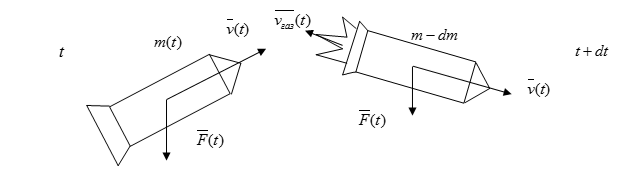
Рисунок 1.
Пусть $m(t)$- масса ракеты в произвольный момент времени $t$, а $v(t)$- ее скорость в тот же момент. Количество движения ракеты в этот момент времени будет $mv$. Спустя время $dt$ масса и скорость ракеты получат приращение $dm$ и $dv$ (величина $dm$ отрицательна). Количество движения ракеты станет равным $(m+dm)(v+dv)$. Сюда надо добавить количество движения газов, образовавшихся за время $dt$. Оно равно $dm_{газ} v_{газ} $, где $dm_{газ} $- масса газов, образовавшихся за время $dt$, а $v_{газ} $- их скорость. Вычитая из суммарного количества движения в момент $t+dt$ количество движения системы в момент времени $t$, найдем приращение этой величины за время $dt$. Это приращение равно $Fdt$, где $F$- геометрическая сумма всех внешних сил, действующих на ракету. Таким образом:
$(m+dm)(v+dv)+dm_{газ} v_{газ} -mv=Fdt$. (1)
Время $dt$ и приращения $dm$ и $dv$ устремим к нулю, т.к. нас интересуют предельные отношения или производные $dm/dt$ и $dv/dt$. Поэтому, раскрывая скобки, можно отбросить произведение $dm\cdot dv$, как бесконечно малую высшего порядка. Далее, ввиду сохранения массы, $dm+dm_{газ} =0$. Пользуясь этим, можно исключить массу газов $dm_{газ} $. А разность $v_{отн} =v_{газ} -v$ есть скорость истечения газов относительно ракеты -- скорость газовой струи. С учетом этих замечаний уравнение (1) преобразуется к виду:
$mdv=v_{отн} dm+Fdt$. (2)
Разделив на $dt$, получаем:
$m\frac{dv}{dt} =v_{отн} \frac{dm}{dt} +F$. (3)
Уравнение Мещерского
По форме уравнение (3) совпадает с уравнением, выражающим второй закон Ньютона. Однако масса тела $m$здесь не постоянна, а меняется во времени из-за потери вещества. К внешней силе $F$ добавляется дополнительный член $v_{отн} \frac{dm}{dt} $, который может быть истолкован как реактивная сила, т.е. сила, с которой действуют на ракету вытекающие из нее газы. Уравнение (3) впервые было получено русским механиком И. В. Мещерским. Оно, так же как и эквивалентное ему уравнение (2), называется уравнением Мещерского или уравнением движения точки с переменной массой.
Формула Циолковского
Применим уравнение (2) к движению ракеты, на которую не действуют никакие внешние силы. Полагая $F=0$, получим:
Допустим, что ракета движется прямолинейно в направлении, противоположном скорости газовой струи $v_{отн} $. Если направление полета принять за положительное, то проекция вектора $v_{отн} $ на это направление будет отрицательной и равной $-v_{отн} $. Поэтому в скалярной форме предыдущее уравнение можно записать так $mdv=v_{отн} dm$. Тогда:
$\frac{dv}{dm} =-\frac{v_{отн} }{m} $ (4)
Скорость газовой струи $v_{отн} $ может меняться во время полета. Однако простейшим и наиболее важным является случай, когда она постоянна. Предположение о постоянстве сильно облегчает решение уравнения (4). В этом случае:
Значение постоянной интегрирования С определяется начальными условиями. Допустим, что в начальный момент времени скорость ракеты равна нулю, а ее масса равна $m_{0} $. Тогда из предыдущего уравнения получаем:
$C=v_{отн} \ln \frac{m_{0} }{m} $ тогда: $v=v_{отн} \ln \frac{m_{0} }{m} $ или $\frac{m_{0} }{m} =e^{\frac{v}{v_{отн} } } $
Последнее соотношение называется формулой Циолковского.
-
Формула Циолковского позволяет рассчитать запас топлива, необходимый, чтобы сообщить ракете скорость $\upsilon $.
-
Величина достигаемой ракетой максимальной скорости не зависит от времени сгорания топлива.
-
Оптимальным путем изменения достигаемой максимальной скорости является увеличение относительной скорости истечения газов.
-
Для получения первой космической скорости при меньшем соотношении между массой ракеты и требуемой массы топлива целесообразно использование многоступенчатых ракет.
Примеры
Космический корабль двигался с постоянной по величине скоростью $v$. Для изменения направления его полета включается двигатель, выбрасывающий струю газа со скоростью $v_{отн} $ относительно корабля в направлении, перпендикулярном к его траектории. Определить угол $\alpha $, на который повернется вектор скорости корабля, если начальная масса его $m_{0} $, а конечная $m$.
Дано: $v$, $v_{отн} $, $m_{0} $, $m$.
Найти: $\alpha $-?
Решение:
Ускорение корабля по абсолютной величине равно:
$a=\omega ^{2} r=\omega v$, причем $v=const$. Поэтому уравнение движения:
$m\frac{dv}{dt} =v_{отн} \frac{dm}{dt} $ переходит в: $mv\omega dt=-v_{отн} dm$.
Так как $d\alpha =\omega dt$ есть угол поворота за время $dt$, интегрируя наше уравнение, получим:
\[\alpha =\frac{v_{отн} }{v} \ln \frac{m_{0} }{m} .\]Ответ: угол поворота вектора скорости равен: $\alpha =\frac{v_{отн} }{v} \ln \frac{m_{0} }{m} $
Ракета перед стартом имеет массу $m_{0} =250$кг. На какой высоте окажется ракета через $t=20$с после начала работы двигателей? Расход топлива равен $\mu =4$кг/с и скорость истечения газов относительно ракеты $v_{отн} $$=1500$м/с постоянны. Поле тяготения Земли считать однородным.
Дано: $m_{0} =250$кг, $t=20$с, $\mu =4$кг/с, $v_{отн}=1500$м/с.
Найти: $H$-?
Решение:
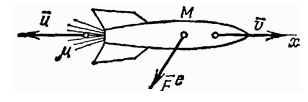
Рисунок 2.
Запишем уравнение Мещерского в однородном поле тяготения Земли в виде:
\[m\frac{\Delta v_{0} }{\Delta t} =\mu v_{отн} -mg,\]где $m=m_{0} -\mu t$, а $v_{0} $- скорость ракеты в момент времени $t$. Разделяя переменные получаем:
\[\Delta v_{0} =(\frac{\mu v_{отн} }{m_{0} -\mu t} -g)\Delta t\]Решение данного уравнения, удовлетворяющего начальному условию $v_{0} =0$ при $t=0$, имеет вид:
\[v_{0} =v_{отн} \ln \frac{m_{0} }{m_{0} -\mu t} -gt\]Учитывая что $H_{0} =0$ при $t=0$ получим:
\[H=v_{отн} t-\frac{gt^{2} }{2} +\frac{v_{отн} m_{0} }{\mu } (1-\frac{\mu t}{m_{0} } )\ln (1-\frac{\mu t}{m_{0} } ).\]Подставляя начальные значения, получаем:
$H=v_{отн} t-\frac{gt^{2} }{2} +\frac{v_{отн} m_{0} }{\mu } (1-\frac{\mu t}{m_{0} } )\ln (1-\frac{\mu t}{m_{0} } )=3177,5$м
Ответ: через $20$с ракета окажется на высоте $H=3177,5$м.











