Существует множество таблиц значений степеней натуральных чисел. Привести их все не представляется возможным. Здесь мы приведем примеры некоторых таких таблиц и задачи на нахождение значений по таким таблицам.
Таблица степеней первых натуральных чисел
Приведем для начала таблицу для нахождения степеней натуральных чисел от $2$ до $12$ по степеням от $1$ до $10$ (таблица 1). Отметим, что мы не приводим степени числа $1$, потому что единица в любой степени будет равняться самой себе.
Находить по этой таблице значения надо следующим образом: В первом столбце находим число, степень которого нас интересует. Запоминаем номер этой строчки. Затем в первой сроке находим показатель степени и запоминаем найденный столбец. Пересечение найденной строки и столбца и даст нам ответ.
Найти $8^7$
Решение.
Находим в первом столбце число $8$: получаем 8-ю строчку.
Находим в первой строке число $7$: получаем 8-й столбец.
Видим, что на их пересечении находится число $2097152$. Следовательно
$8^7=2097152$
Таблицы степеней натуральных чисел от $1$ до $100$
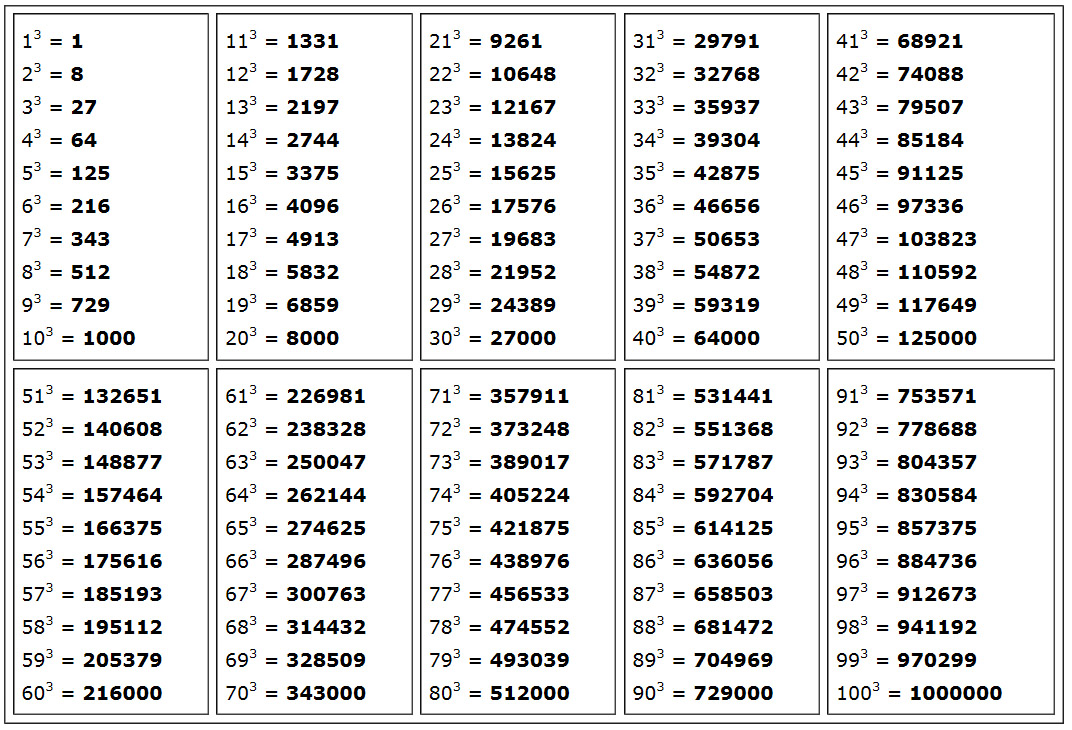
Также довольно популярны таблицы степеней от $1$ до $100$. Все их привести невозможно, поэтому мы здесь приведем для примера такие таблицы для квадратов и кубов таких натуральных чисел (таблица 2 и таблица 3).
Эти таблицы напоминают всем известные таблицы умножения, поэтому, мы думаем, читателю не составит труда использование данных таблиц.
Найти
а) $76^2$.
б) $28^3$
Решение.
а) Данное значение находим в таблице $2$ в $8$ табличке:
$76^2=5776$
б) Данное значение находим в таблице $3$ в $3$ табличке:
$28^3=21952$
Таблица квадратов натуральных чисел от $10$ до $99$
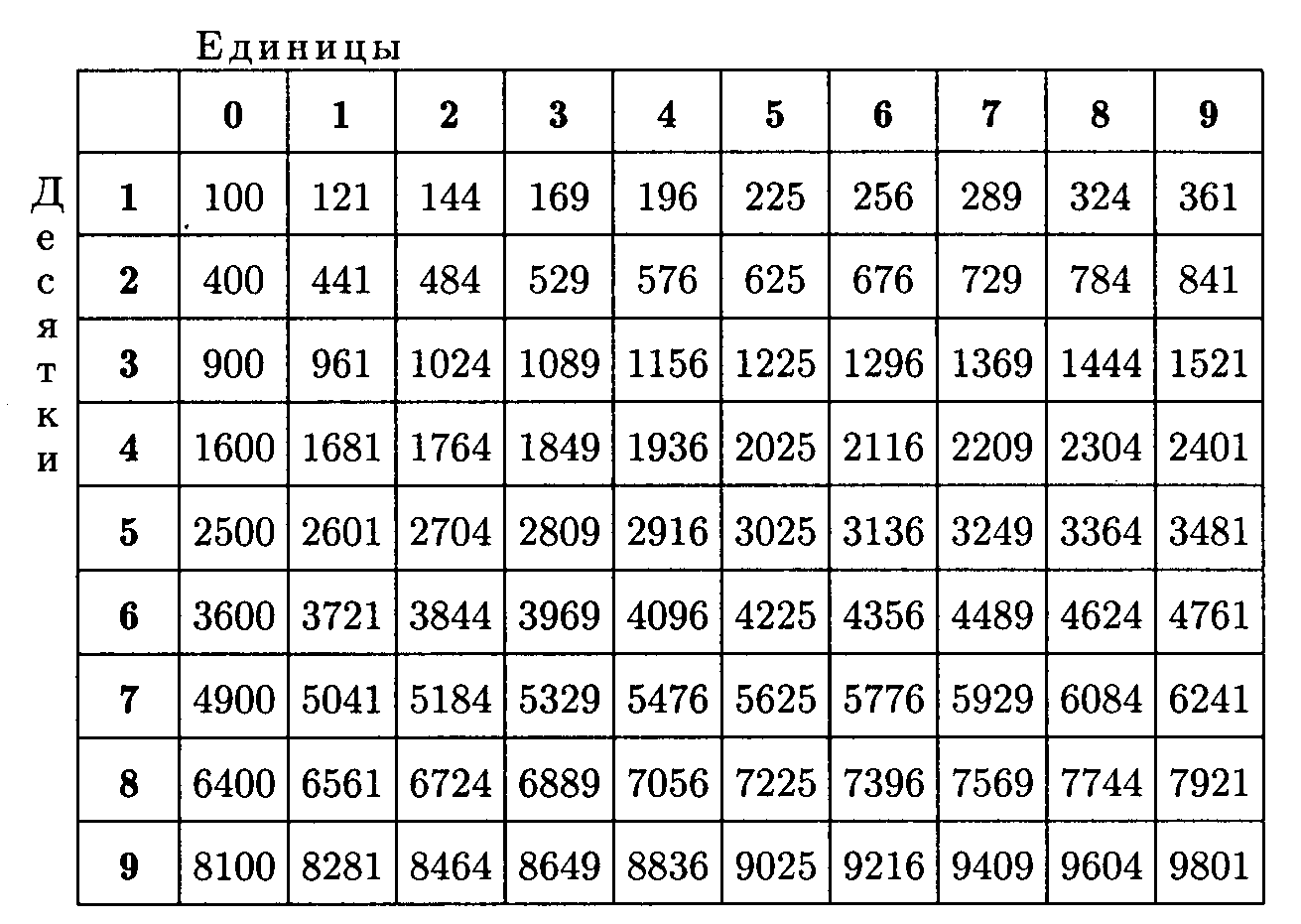
Еще одной пользующейся популярностью таблицей является таблица квадратов чисел от $10$ до $99$ (таблица 4), то есть всех десятичных чисел.
Находить по этой таблице значения надо следующим образом: В первом столбце находим число десятков интересующего нас числа. Запоминаем номер этой строчки. Затем в первой сроке находим число единиц интересующего числа и запоминаем найденный столбец. Пересечение найденной строки и столбца и даст нам ответ.
Найти $37^2$
Решение.
Находим в первом столбце число $3$: получаем 4-ю строчку.
Находим в первой строке число $7$: получаем 8-й столбец.
Видим, что на их пересечении находится число $1369$. Следовательно
$37^2=1369$