Генеральная средняя
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Генеральная совокупность -- совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Генеральная средняя -- среднее арифметическое значений вариант генеральной совокупности.
Пусть значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$. Тогда генеральная средняя вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1,\ x_2,\dots ,x_k$ различны. В этом случае $n_1,\ n_2,\dots ,n_k=1$. Получаем, что в этом случае генеральная средняя вычисляется по формуле:
Выборочная средняя
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Выборочная совокупность -- часть отобранных объектов из генеральной совокупности.
Выборочная средняя -- среднее арифметическое значений вариант выборочной совокупности.
Пусть значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$. Тогда выборочная средняя вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1,\ x_2,\dots ,x_k$ различны. В этом случае $n_1,\ n_2,\dots ,n_k=1$. Получаем, что в этом случае выборочная средняя вычисляется по формуле:
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной средних значений за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Примеры задач на нахождение средней выборки
В магазин завезли 10 видов шоколадных конфет. По ним проведена следующая выборка по цене за килограмм: 70, 65, 97, 83, 120, 107, 77, 88, 100, 86. Построить ряд распределения данной генеральной совокупности и найти её генеральное среднее.
Решение.
Видим, что все значения вариант различны, поэтому частоты равны единице. Ряд распределения можно записать следующим образом, перечислив значения вариант в порядке возрастания:
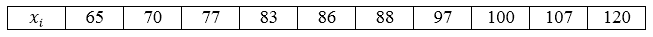
Рисунок 1.
Так как наша совокупность является генеральной и все варианты различны, то мы будем пользоваться следующей формулой:
\[\overline{x_г}=\frac{\sum\limits^k_{i=1}{x_i}}{n}\]Получим:
\[\overline{x_г}=\frac{65+70+77+83+86+88+97+100+107+120}{10}=89,3\]Ответ: 89,3.
Выборочная совокупность задана следующей таблицей распределения:

Рисунок 2.
Найти среднее выборочное данной совокупности.
Решение.
Для нахождения значения выборочной средней будем пользоваться следующей формулой:
\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}\]Обычно, для наглядности и удобности вычислений составляется расчетная таблица, в которую входят необходимые промежуточные вычисления. В нашем случае составим таблицу со следующей «шапкой»:
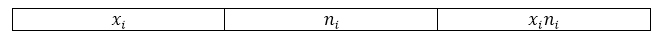
Рисунок 3.
Внизу таблицы также добавляется строка «итог», в которой подсчитывается сумма по всем значениям столбцов. Проведя необходимые вычисления, получим следующую расчетную таблицу:

Рисунок 4.
Используя формулу, получим:
\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}=\frac{305}{20}=15,25\]Ответ: 15,25.
Проводится социальный опрос среди 100 пенсионеров об уровне их пенсии. Получена следующая таблица распределения результатов опроса (размер пенсии указан в тысячах рублей):

Рисунок 5.
Найти среднее выборочное данной совокупности.
Данная совокупность является выборочной, поэтому будем пользоваться следующей формулой:
\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}\]Составим, для начала, расчетную таблицу.
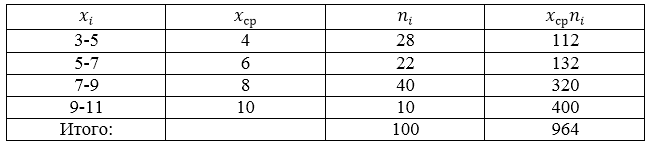
Рисунок 6.
Получаем:
\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}=\frac{964}{100}=9,64\]Ответ: 9,64.











