Напомним, что вероятность попадания непрерывной случайной величины в интервал $(\alpha ,\beta )$ находится по формуле:
величины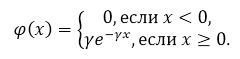
Рисунок 1.
где $\gamma $ - положительная константа.
Напомним, что функция распределения показательной вероятности имеет следующий вид:
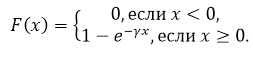
Рисунок 2.
где $\gamma $ - положительная константа.
Тогда:
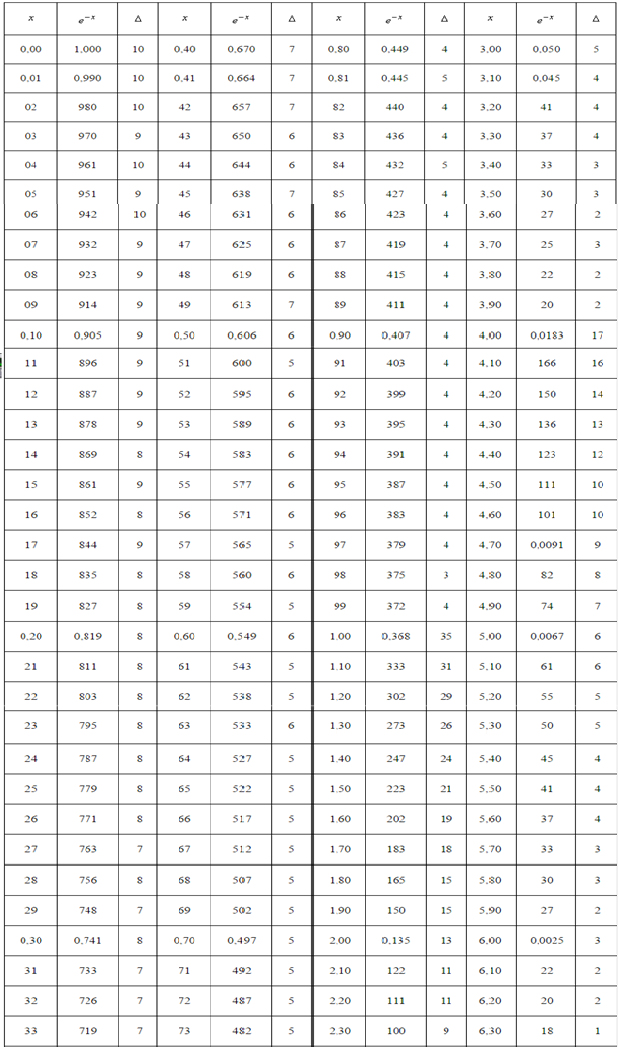
Рисунок 3. Значения функции $y=e^{-x}$
Примеры решения задач на нахождение вероятности попадания случайной величины в заданный интервал
Непрерывная случайная величина $X$ подчиняется показательному закону распределения. На промежутке $[0,\infty )$ плотность распределения имеет вид: $\varphi \left(x\right)=5e^{-\alpha x}.$
Найти:
- Коэффициент $\alpha $.
- Плотность распределения.
- Функция распределения.
- Найти вероятность того, что случайная величина попадет в интервал $(0,1)$.
Решение:
- Так как распределения является показательным, то по формуле плотности распределения $\alpha =5$.
- По формуле плотности распределения, получим:
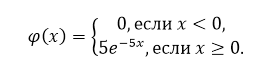
Рисунок 4.
- По формуле функции распределения, имеем:
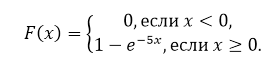
Рисунок 5.
- Найдем вероятность по формуле:
Работа телефонного аккумулятора имеет показательное распределение с коэффициентом $\gamma =0,04$. Определить:
- Вероятность того, что телефон разрядится через 70 часов.
- Вероятность того, что за это время телефон не разрядится.
Решение:
Воспользуемся формулой $P\left(\alpha
- Найти вероятность того, что телефон разрядится равносильно тому, чтобы найти вероятность попадания случайной величины в интервал $(0,70)$:
Тогда вероятность того, что он не разрядится, равна
\[100\%-24,4\%=75,6\%\]10\% телевизоров ломаются в течении первых 4000 часов работы. Найти вероятность, что телевизор сломается в интервале от 1000 до 2000 часов работы. (Распределение считать экспоненциальным)
Решение:
По определению потенциального распределения, плотность распределения имеет вид:
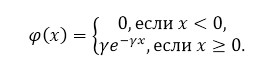
Рисунок 6.
Для начала необходимо найти константу $\gamma $. Из условия задачи, получаем:
\[P\left(X\ge 4000\right)=0,1.\]Найдем $P\left(X\ge 4000\right)$:
\[P\left(X\ge 4000\right)=1-P\left(XКак нам уже известно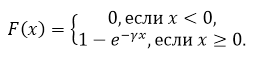
Рисунок 7.
Значит
\[F\left(4000\right)=1-e^{-4000\gamma }\]Получаем уравнение:
\[1-1+e^{-4000\gamma }=0,1,\] \[e^{-4000\gamma }=0,1,\] \[-4000\gamma =ln0,1,\] \[\gamma =-\frac{ln0,1}{4000}=0,00058\]Получаем, что плотность распределения имеет вид:
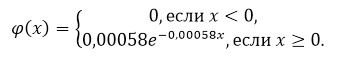
Рисунок 8.
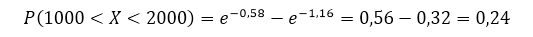
Рисунок 9.
Ответ: $24\%$.












