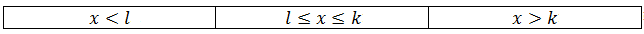Понятие модуля
Для начала вспомним, собственно, что такое модуль.
Модулем будем называть такую математическую конструкцию, при которой действительное неотрицательное число совпадает с самим числом, а отрицательное равняется абсолютному значению этого числа.
Обозначение: $|x|$.
Математически это выглядит следующим образом:
$|x|=\cases{x,x≥0,\\-x,x
Пример: $|-31|=31$
Очевидно из определения, что модуль всегда будет неотрицательным числом.
Далее рассмотрим некоторые возможные виды уравнений с модулем и их общие решения.
Уравнение $|f(x) |=θ$
Рассмотрим уравнение
$|f(x)|=θ$
Здесь $θ$ – какое-то действительное число. Решение такого уравнения зависит от значения этого числа, поэтому рассмотрим три случая.
Если $θ>0$, то уравнение будет иметь следующие два решения:
$f(x)=θ$ и $f(x)=-θ$
Если $θ=0$, то уравнение будет иметь ровно 1 решение:
$f(x)=0$
Если $θ
Решить
$|πx^2 |=π$
Решение.
Так как число $π>0$, уравнение будет иметь решения
Первое решение
$πx^2=π$
$x=±1$
Второе решение
$πx^2=-π$
$x^2=-1$ - корней нет.
Ответ: $±1$.
Уравнение $|f(x) |=q(x)$
Рассмотрим уравнение
$|f(x)|=q(x)$
Так как, из определения 1, модуль всегда неотрицателен, здесь, в первую очередь, надо найти область определения.
ООУ: $q(x)≥0$
Далее, решение такого уравнения будет равносильно решению следующих двух систем:
$\cases{f(x)≥0,\\f(x)=q(x).}$ и $\cases{f(x)
Решить
$|3x^2+6|=x+6$
Решение.
Найдем для начала область определения:
ООУ: $x≥-6$
Теперь запишем для решения две системы:
$\cases{3x^2+6≥0,\\3x^2+6=x+6.}$ и $\cases{3x^2+6
Вторая система решений иметь не будет, так как выражение $3x^2+6$ всегда положительно.
Найдем корни первой системы:
$3x^2+6=x+6$
$x(3x-1)=0$
$x=0$ и $x=\frac{1}{3}$
Ответ: $0$ и $\frac{1}{3}$.
Замечание: Отметим, что составлением равносильных совокупностей можно решать и некоторые другие уравнения с модулем, поэтому это можно считать одним из способов решения таких уравнений.
Уравнение $|f(x) |=|q(x)|$
Решение такого уравнения удобно рассматривать с помощью таблицы.
Для того, чтобы сделать «шапку» это таблицы найдем для начала корни всех выражений, которые содержатся под знаком модуля. Пусть у нас при $f(x)=0$ будет $x=l$, а при $q(x)=0$ будет $x=k$. Без ограничения общности предположим, что $l
Далее нам остается рассмотреть решения этого уравнения на каждом полученном промежутке.

Останется записать правильный ответ.
Решить
$|3-4x|=|5-6x|$
Решение.
Найдем корни выражений под модулями:
$3-4x=0$ и $5-6x=0$
$x=\frac{3}{4}$ и $x=\frac{5}{6}$
Составляем таблицу:

Окончательно
Ответ: $\frac{4}{5}$ и $1$.
Замечание: Отметим, что этим способом можно разрешать любые уравнения, содержащие модуль. Такой способ называется методом промежутков или методом интервалов.