-
График $y=f(x-a)$ будем строить с помощью графика $f(x)$ сдвигая его вдоль оси $Ox$ на значение $|a|$ вправо, если $a >0$ и на это же значение влево, если $a
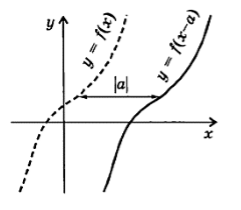
Рисунок 1. -
График $y=f(x)+b$ будем строить с помощью графика $f(x)$ сдвигая его вдоль оси $Oy$ на значение $|b|$ вверх, если $b >0$ и на тоже значение вниз, если $\ b
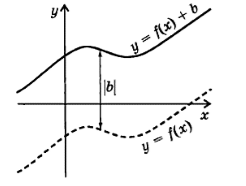
Рисунок 2. -
График $y=f(kx)$ будем строить с помощью графика $f(x)$ сжимая его к оси $Oy$, если $k >1$ и растягивая, если $0
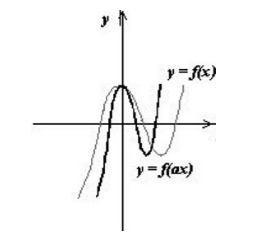
Рисунок 3. -
График $y=kf(x)$ будем строить с помощью графика $f(x)$ растягивая его от оси $Ox$ в $k$ раз, если $k >1$ и сжимая к оси $Ox$ в $\frac{1}{k}$ раз, если $0
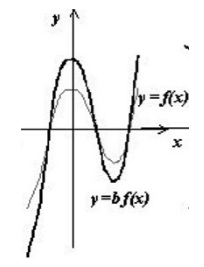
Рисунок 4. -
График $y=f(x)$ будем строить с помощью графика $f(x)$ симметрично отображая его относительно оси $Oy$ (рис. 5).
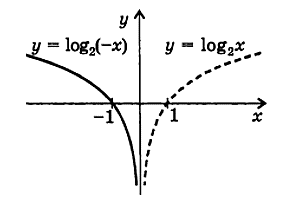
Рисунок 5. -
График $y=-f(x)$ будем строить с помощью графика $f(x)$ симметрично отображая его относительно оси $Ox$ (рис.6).
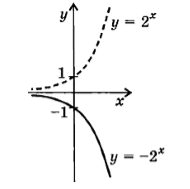
Рисунок 6. -
График $y{\mathbf =|}f(x){\mathbf |}$ будем строить с помощью графика $f(x)$ следующим образом: та часть графика $f(x)$, которая лежит над осью $Ox$ остается неизменна, а которая лежит под $Ox$ будет отображаться симметрично относительно оси $Oy$
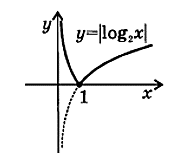
Рисунок 7. -
График $y=f(|x|)$ будем строить с помощью графика $f(x)$ следующим образом: та часть графика $f(x)$, которая лежит справа от оси $Oy$ остается неизменна, а потом эта же часть будет отображаться симметрично относительно оси $Oy$, полностью заменяя часть, лежащую слева от $Oy$ (рис. 8).
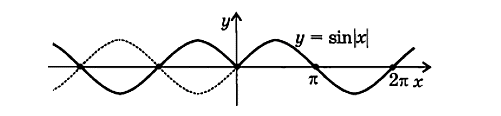
Рисунок 8.
Пример задачи
Построить графики функций $y=sin3x$ и $y=-sin3x.$
Решение.
Будем производить все построения на одном рисунке. Первым этапом построим график функции $y={\sin x\ }$. На рисунке 9 данная функция изображена мелким пунктиром.
После этого построим график функции $y=sin3x$ по правилу 3 выше. На рисунке 9 этот график изображен крупным пунктиром.
Последним этапом из графика функции $y=sin3x$ получаем график функции $y=-sin3x$ по правилу 6, описанном выше. На рисунке 9 данный график изображен сплошной линией.
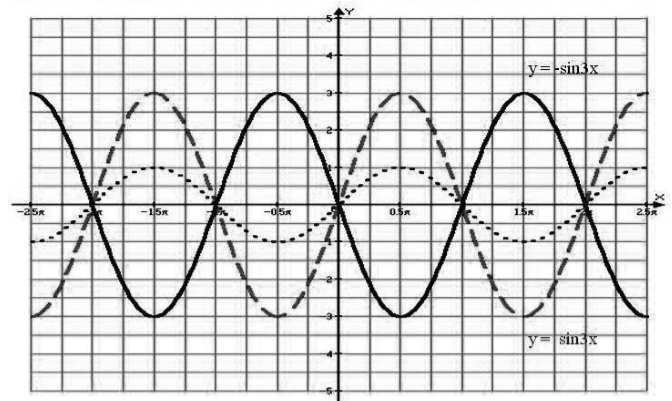
Рисунок 9.











