Позиционная система счисления представляет собой такую систему счисления, у которой значение любой цифры в числе зависит от ее положения в ряду цифр, изображающих это число.
Основными достоинствами позиционных систем счисления являются:
-
простое выполнение арифметических операций;
-
при записи числа используется малое количество символов.
Данная система записи чисел отличается удобством и экономичностью, причем не только для фиксирования чисел на бумажных носителях и для выполнения действий с ними, но и для механического представления чисел. Так, например, в счетах каждому разряду числа соответствует металлический стержень, являющийся своеобразной направляющей, по которой можно передвигать костяшки, и они могут занимать одну из десяти позиций.
С практической точки зрения можно использовать (что и делалось в прошлом веке) и другие варианты физического представления чисел:
-
С помощью нескольких колес, каждое из которых фиксируется в одном из десяти возможных положений.
-
В вычислительных машинах первых поколений широко использовались перфокарты, своеобразные карточки, размеченные рядами цифр, которые при записи программ пробивались в определенных позициях, т.е. кодировались. Одна программа, которую считывала машина, могла состоять из десятков и даже сотен перфокарт.
Все подобные представления можно объединить общим фактом. Это то, что физический носитель состоит из определенного числа однородных элементов, которые, в свою очередь, могут находиться в одном из десяти состояний. Эти состояния можно назвать разрядами, т.е. это позиции цифр в числе.
Важной характеристикой любых позиционных систем счисления является основание, которое представляет собой количество различных цифр, использующихся для отображения чисел в данной системе.
В качестве основания используются натуральные числа — $2$, $8$, $10$ и др., в результате с использованием любого нового числа образовывается новая позиционная система: двоичная, восьмеричная, десятичная и ... т.д.
Позиционная система счисления определяется путем группировки целых и дробных чисел, при этом получается вещественное число, которое можно представить в виде:
$Aq = ±(a_{n-1} q^{n-1} + a_{n-2} q^{n-2} + … a_0q^0 + a_{-1}q^{-1} + a_{-2}q^{-2} + … a_{-m}q^{-m})$,
где:
-
$A$ – число;
-
$q$ – основание системы счисления:
-
$ai$ – цифры данной системы счисления;
-
$n$ – число разрядов целой части числа;
-
$m$ – число разрядов дробной части.
Расписать в соответствии с приведенной выше формулой число $A_{10} = 8754,32$.
Решение:
$A_{10} = 8\cdot 10^3 + 7\cdot 10^2 + 5\cdot 10^1 + 4\cdot 10^0 + 3\cdot 10^{-1} + 2\cdot 10^{-2} = 8754, 32$
Существенным отличием позиционных систем от непозиционных является необходимость использования специального знака «нуля» для обозначения пропущенных разрядов.
Данных систем большое количество, поскольку за основание системы счисления можно принять любое число не менее $2$.
Позиционные системы счисления классифицируют по основанию на:
- Двоичные (имеют в основании две цифры $0$ и $1$).
- Восьмеричные (в основании цифры от $0$ до $7$).
- Десятичные (в основании цифры от $0$ до $9$).
- Шестнадцатеричные (в основании цифры от $0$ до $9$ и буквы $A$, $B$, $C$, $D$, $E$, $F$).
- Пятеричная (в основании цифры от $0$ до $4$, используется в Китае и в настоящее время).
- Двенадцатеричная (в основании цифры от $0$ до $9$ и буквы $A$, $B$ устаревшая, использовалась в начале $XX$ века).
- Шестидесятеричная.
- Двадцатеричная.
В настоящее время используются: двоичная, восьмеричная, десятичная, шестнадцатеричная системы и при измерении времени и углов шестидесятеричная система.
Другие же приведенные выше системы счисления устарели и не используются.
Рассмотрим примеры некоторых из них.
Вавилонская десятеричная / шестидесятеричная
В древнем Вавилоне примерно во $II$ тысячелетие до нашей эры использовалась система счисления, в которой числа менее $60$ обозначались с помощью двух знаков:

Рисунок 1. для единиц,
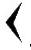
Рисунок 2. для десятков
Они имели клинообразный вид, поскольку жители Вавилона писали на глиняных табличках палочками треугольной формы. Знаки в записях повторяли определенное количество раз, например:
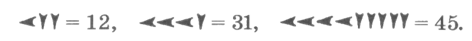
Рисунок 3.
Все число в целом записывалось в позиционной системе счисления с основанием $60$. Приведем примеры:

Рисунок 4. Эта запись обозначала $6\cdot 60 + 3 = 363$, можно сравнить с записью числа $63$: $6\cdot 10 + 3$

Рисунок 5. Эта запись обозначала $32\cdot 60 + 52 = 1972$
Шестидесятеричная запись целых чисел не получила широкого распространения за пределами Ассиро-вавилонского царства, но шестидесятеричные дроби применяются до сих пор при измерении времени. Например, одна минута = $60$ секунд, один час = $60$ минут.
Древнекитайская десятеричная
Данная система счисления - самая прогрессивная из старейших, так как она построена на тех же принципах, что и современная «арабская», используемая в наше время. Возникла эта система около $4 000$ тысяч лет назад в Китае.

Рисунок 6.
Числа в ней записывались слева направо, от большего к меньшему. При отсутствии какого-либо разряда ничего не ставили и переходили к следующему, такой разряд во времена правления династии Мин стал обозначаться кружочком, аналогом нуля. Во избежание путаницы разрядов ввели несколько служебных иероглифов, которые записывались после основного и показывали, какое значение принимает иероглиф-цифра в данном разряде.
Двадцатеричная система счисления индейцев Майя
Эта система интересна тем, что развивалась самостоятельно, без влияния цивилизаций Европы и Азии. Ее использовали в качестве календаря и для астрономических наблюдений. Характерная особенность данной системы счисления - наличие нуля, который изображался в виде ракушки. Основание системы - число $20$, при этом наблюдаются признаки пятеричной системы. Первые $19$ чисел системы получали комбинированием точек (один) и черточек (пять).
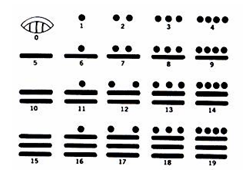
Рисунок 7.
Число $20$ изображалось из двух цифр, ноль и один наверху и называлось уиналу (рис.8).
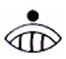
Рисунок 8.
Записывали числа столбцами, при это низшие разряды располагали внизу, а высшие - наверху, в результате чего получалось своеобразное изображение этажерки с полками. Если число ноль появлялось без единицы наверху, то это обозначало, что единицы данного разряда отсутствуют. Пример получения числа в такой системе:
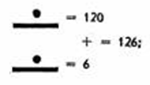
Рисунок 9.
В двадцатеричной системе счета древних майя имелось исключение, проявлявшееся в случае прибавления к числу $359$ одной единицы первого порядка. Суть исключения заключалась в следующем: $360$ является начальным числом третьего порядка и его место уже не на второй, а на третьей полке.
Но при этом получается, что начальное число третьего порядка больше начального числа второго не в двадцать раз ($20\cdot 20=400$, а не $360!$), а только в восемнадцать. Отсюда следует, что принцип двадцатеричности нарушен.
Ответ заключается в том, что у индейцев Майя $20$ дней-кинов образовывали месяц или уинал. $18$ месяцев-уиналов образовывали год или туну ($360$ дней в году) и так далее.
Это довольно сложная система счисления использовалась жрецами для астрономических наблюдений, другая система индейцев Майя была аддитивной, похожей на египетскую и применялась в повседневной жизни.











