Десятичное и двоичное представление чисел
Для работы с числовой информацией мы пользуемся системой счисления, содержащей десять цифр: от $0$ до $9$. Эта система называется десятичной.
Кроме цифр, в десятичной системе большое значение имеют разряды. Подсчитывая количество чего-нибудь и дойдя до самой большой из доступных нам цифр (до $9$), мы вводим второй разряд и дальше каждое последующее число формируем из двух цифр. Дойдя до $99$, мы вынуждены вводить третий разряд. В пределах трех разрядов мы можем досчитать уже до $999$ и т.д.
Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.
Компьютер ведет подсчет аналогичным образом, но имеет в своем распоряжении всего две цифры - логический ноль (отсутствие у бита какого-то свойства) и логическую единицу (наличие у бита этого свойства).
Система счисления, использующая только две цифры, называется двоичной. При подсчете в двоичной системе добавлять каждый следующий разряд приходится гораздо чаще, чем в десятичной.
Вот таблица первых десяти чисел в каждой из этих систем счисления:
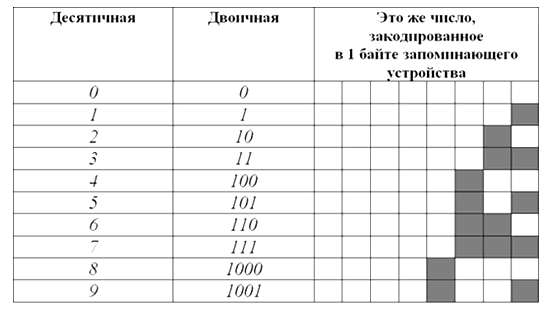
Рисунок 1.
Как видите, в десятичной системе счисления для отображения любой из первых десяти цифр достаточно $1$ разряда. В двоичной системе для тех же целей потребуется уже $4$ разряда.
Соответственно, для кодирования этой же информации в виде двоичного кода нужен носитель емкостью как минимум $4$ бита ($0,5$ байта). Человеческий мозг, привыкший к десятичной системе счисления, плохо воспринимает систему двоичную. Хотя обе они построены на одинаковых принципах и отличаются лишь количеством используемых цифр. В двоичной системе точно так же можно осуществлять любые арифметические операции с любыми числами. Главный ее минус - необходимость иметь дело с большим количеством разрядов.
Так, самое большое десятичное число, которое можно отобразить в 8 разрядах двоичной системы - $255$, в $16$ разрядах – $65535$, в $24$ разрядах – $16777215$.
Алгоритмы кодирования чисел в двоичной системе счисления
Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:
-
Небольшие целые числа без знака.
Для сохранения каждого такого числа на запоминающем устройстве, как правило, выделяется $1$ байт ($8$ битов). Запись осуществляется в полной аналогии с двоичной системой счисления.
Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:
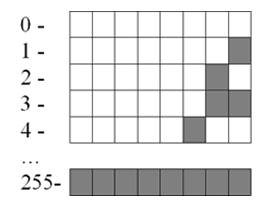
Рисунок 2. -
Большие целые числа и числа со знаком.
Для записи каждого такого числа на запоминающем устройстве, как правило, отводится $2$-байтний блок ($16$ битов).
Старший бит блока (тот, что крайний слева) отводится под запись знака числа и в кодировании самого числа не участвует. Если число со знаком "плюс", этот бит остается пустым, если со знаком "минус" – в него записывается логическая единица. Число же кодируется в оставшихся 15 битах. Например, алгоритм кодирования числа $+2676$ будет следующим:
- Перевести число $2676$ из десятичной системы счисления в двоичную. В итоге получится $101001110100$;
- Записать полученное двоичное число в первые $15$ бит $16$-битного блока (начиная с правого края). Последний, $16$-й бит, должен остаться пустым, поскольку кодируемое число имеет знак $+$.
В итоге $+2676$ в двоичном коде на запоминающем устройстве будет выглядеть так:
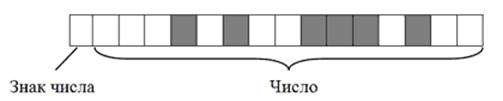
Рисунок 3.Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.
Чтобы было понятно, рассмотрим алгоритм кодирования числа $-2676$:
- Перевести число $2676$ из десятичной системы счисления в двоичную. Получим все тоже двоичное число $101001110100$;
- Записать полученное двоичное число в первые $15$ бит $16$-битного блока. Затем инвертировать, то есть, изменить на противоположное, значение каждого из $15$ битов;
- Записать в $16$-й бит логическую единицу, поскольку кодируемое число имеет отрицательное значение.
В итоге $-2676$ на запоминающем устройстве в двоичном коде будет иметь следующий вид:
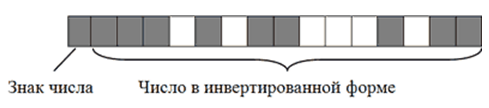
Рисунок 4.Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.
Максимальным десятичным числом, которое можно закодировать в $15$ битах запоминающего устройства, является $32767$. Иногда для записи чисел по этому алгоритму выделяются $4$-байтные блоки. В таком случае для кодирования каждого числа будет использоваться $31$ бит плюс $1$ бит для кодирования знака числа. Тогда максимальным десятичным числом, сохраняемым в каждую ячейку, будет $2147483647$ (со знаком плюс или минус).
-
Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых чисел с плавающей запятой (точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.
Для записи каждого числа с плавающей запятой компьютер чаще всего выделяет $4$-байтную ячейку ($32$ бита):
- в старшем бите этой ячейки (тот, что крайний слева) записывается знак числа. Если число отрицательное, в этот бит записывается логическая единица, если оно со знаком "плюс" – бит остается пустым.
- во втором слева бите аналогичным образом записывается знак порядка (что такое порядок поймете позже);
- в следующих за ним $7$ битах записывается значение порядка.
- в оставшихся $23$ битах записывается так называемая мантисса числа.

Рисунок 5.Чтобы стало понятно, что такое порядок, мантисса и зачем они нужны, переведем в двоичный код десятичное число $6,25$.
Порядок кодирования будет примерно следующим:
- Перевести десятичное число в двоичное (десятичное $6,25$ равно двоичному $110,01$);
- Определить мантиссу числа. Для этого в числе необходимо передвинуть запятую в нужном направлении, чтобы слева от нее не осталось ни одной единицы. В нашем случае запятую придется передвинуть на три знака влево. В итоге, получим мантиссу, $11001$;
- Определить значение и знак порядка. Значение порядка – это количество символов, на которое была сдвинута запятая для получения мантиссы. В нашем случае оно равно $3$ (или $11$ в двоичной форме);
Знак порядка – это направление, в котором пришлось двигать запятую: влево – "плюс", вправо – "минус". В нашем примере запятая двигалась влево, поэтому знак порядка – "плюс".
Таким образом, порядок двоичного числа $110,01$ будет равен $+11$, а его мантисса, $11001$. В результате в двоичном коде на запоминающем устройстве это число будет записано следующим образом

Рисунок 6.
Обратите внимание, что мантисса в двоичном коде записывается, начиная с первого после запятой знака, а сама запятая упускается. Числа с плавающей запятой, кодируемые в $32$ битах, называю числами одинарной точности. Когда для записи числа $32$-битной ячейки недостаточно, компьютер может использовать ячейку из $64$ битов. Число с плавающей запятой, закодированное в такой ячейке, называется числом двойной точности.












