Понятие предиката
Предикат - утверждение, которое содержит переменные, принимающие значение $1$ или $0$ (истинно или ложно) в зависимости от значений переменных.
Например, выражение $x=x^5$ является предикатом, т.к. оно является истинным при $x=0$ или $x=1$ и ложным при всех остальных значениях $x$.
Множество, на котором предикат принимает только истинные значения, называется множеством истинности предиката $I_p$.
Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.
Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:
$P (x_1, \dots, x_n)=1$
Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:
$P (x_1, \dots, x_0)=0$
Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.
Т.к. предикаты могут принимать только два значения (истинно/ложно или $0/1$), то к ним можно применять все операции алгебры логики: отрицание, конъюнкция, дизъюнкция и т.д.
Примеры предикатов
Пусть предикат $R(x, y)$: $«x = y»$ обозначает отношение равенства, где $x$ и $y$ принадлежат множеству целых чисел. В этом случае предикат R будет принимать истинное значение для всех равных $x$ и $y$.
Другой пример предиката -- РАБОТАЕТ($x, y, z$) для отношения «$x$ работает в городе y в компании $z$».
Еще один пример предиката -- НРАВИТСЯ($x, y$) для «x нравится y» для $x$ и $y$, которые принадлежат $M$ -- множеству всех людей.
Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.
Операции над предикатами
Рассмотрим применение операций алгебры логики к предикатам.
Конъюнкция двух предикатов $A(x)$ и $B(x)$ -- предикат , который принимает истинное значение при тех и только тех значениях $x$ из $T$, при которых каждый из предикатов принимает истинное значение, а ложное значение -- во всех остальных случаях. Множество истинности $T$ предиката -- пересечение множеств истинности предикатов $A(x)$ и $B(x)$. Например: предикат $A(x)$: «$x$ -- чётное число», предикат $B(x)$: «$x$ делится на $5$». Таким образом, предикатом будет выражение «$x$ -- чётное число и делится на $5$» или «$x$ делится на $10$».
Дизъюнкция двух предикатов $A(x)$ и $B(x)$ -- предикат , который принимает ложное значение при тех и только тех значениях $x$ из $T$, при которых каждый из предикатов принимает ложное значение и принимает истинное значение во всех остальных случаях. Множество истинности предиката -- объединение областей истинности предикатов $A(x)$ и $B(x)$.
Отрицание предиката $A(x)$ -- предикат, который принимает истинное значение при всех значениях $x$ из $T$, при которых предикат $A(x)$ принимает ложное значение и наоборот. Множество истинности предиката $A(x)$ -- дополнение $T'$ к множеству $T$ в множестве $x$.
Импликация предикатов $A(x)$ и $B(x)$ -- предикат , который является ложным при тех и только тех значениях $x$ из $T$, при которых $A(x)$ -- истинно, а $B(x)$ -- ложно, и принимает истинное значение во всех остальных случаях. Читается: «Если $A(x)$, то $B(x)$».
Пусть $A(x)$: «Натуральное число $x$ делится на $3$»;
$B(x)$: «Натуральное число $x$ делится на $4$».
Составим предикат: «Если натуральное число $x$ делится на $3$, то оно делится и на $4$».
Множество истинности предиката -- объединение множества истинности предиката $B(x)$ и дополнения к множеству истинности предиката $A(x)$.
Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.
Кванторы
Кванторы -- логические операторы, применение которых к предикатам превращает их в ложные или истинные высказывания.
Квантор -- логические операции, которые ограничивают область истинности предиката и создают высказывание.
Чаще всего используют кванторы:
-
квантор всеобщности (обозначается символом $\forall x$) -- выражение «для всех $x$» («для любого $x$»);
-
квантор существования (обозначается символом $\exists x$) -- выражение «существует $x$ такое, что... »;
-
квантор единственности и существования (обозначается $\exists !x$) -- выражение «существует точно одно такое $x$, что... ».
В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.
Примеры применения кванторов
Пусть -- предикат «$x$ кратно $7$».
С помощью квантора всеобщности можно записать следующие ложные высказывания:
-
любое натуральное число делится на $7$;
-
каждое натуральное число делится на $7$;
-
все натуральные числа делятся на $7$;
который будет иметь вид:
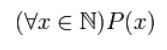
Рисунок 1.
Для записи истинных высказываний используем квантор существования:
-
существуют натуральные числа, которые делятся на $7$;
-
найдётся натуральное число, которое делится на $7$;
-
хотя бы одно натуральное число делится на $7$.
Запись будет иметь вид:
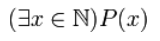
Рисунок 2.
Пусть на множестве $x$ простых чисел задан предикат : «Простое число является нечетным». Поставив перед предикатом слово «любое», получим ложное высказывание: «Любое простое число является нечетным» (например, $2$ является простым четным числом).
Поставим перед предикатом слово «существует» и получим истинное высказывание: «Существует простое число , которое является нечетным» (например, $x=3$ ).
Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.
Операции над кванторами
Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:
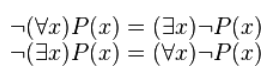
Рисунок 3.
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:
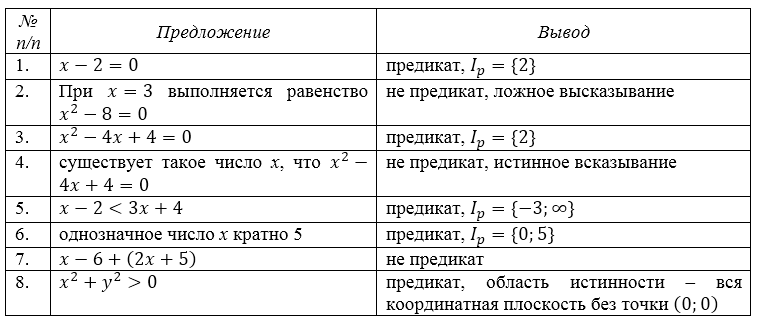
Рисунок 4.











