Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:
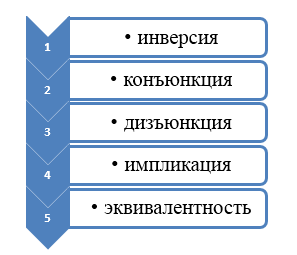
Рисунок 1.
Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
-
Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
-
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
-
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
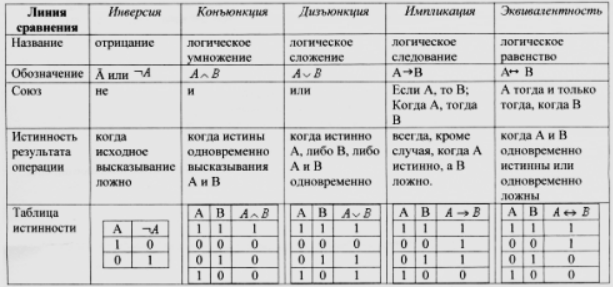
Рисунок 2.
Составить таблицу истинности логического выражения $D=\bar{A} \vee (B \vee C)$.
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- инверсия ($\bar{A}$);
- дизъюнкция, т.к. она находится в скобках ($B \vee C$);
-
дизъюнкция ($\overline{A}\vee \left(B\vee C\right)$) – искомое логическое выражение.
Кол-во столбцов = $3 + 3=6$.
-
Заполним таблицу, учитывая таблицы истинности логических операций.
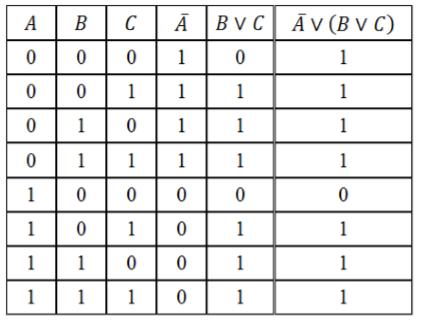
Рисунок 3.
По данному логическому выражению построить таблицу истинности:
\[F=\overline{(A\vee B)\bigwedge \overline{C}}\vee \overline{(A\vee C)\bigwedge B}\]Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- отрицание ($\bar{C}$);
- дизъюнкция, т.к. она находится в скобках ($A \vee B$);
- конъюнкция ($(A\vee B)\bigwedge \overline{C}$);
- отрицание, которое обозначим $F_1$ ($\overline{(A\vee B)\bigwedge \overline{C}}$);
- дизъюнкция ($A \vee C$);
- конъюнкция ($(A\vee C)\bigwedge B$);
- отрицание, которое обозначим $F_2$ ($\overline{(A\vee C)\bigwedge B}$);
-
дизъюнкция – искомая логическая функция ($\overline{(A\vee B)\bigwedge \overline{C}}\vee \overline{(A\vee C)\bigwedge B}$).
Кол-во столбцов = $3 + 8 = 11$.
-
Заполним таблицу, учитывая таблицу истинности логических операций.
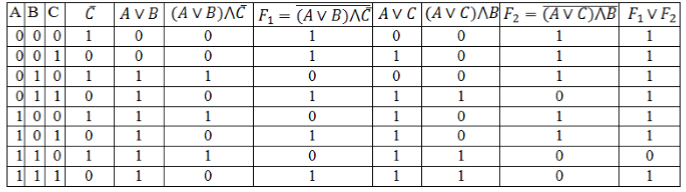
Рисунок 4.
Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.
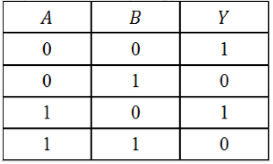
Рисунок 5.
Решение:
- Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
- Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:
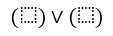
Рисунок 6. - Каждое логическое выражение в этой дизъюнкции запишем как конъюнкцию аргументов функции $A$ и $B$: $\left(A\wedge B\right)\vee \left(A\wedge B\right)$
- В случае, когда значение в соответствующей строке таблицы равно $0$, запишем этот аргумент с отрицанием, получим искомую функцию:\[Y\left(A,B\right)=\left(\overline{A}\wedge \overline{B}\right)\vee \left(A\wedge \overline{B}\right).\]











