Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.
Нормальная форма существует в двух видах:
-
конъюнктивная нормальная форма (КНФ) -- конъюнкция нескольких дизъюнкций, например, $\left(A\vee \overline{B}\vee C\right)\wedge \left(A\vee C\right)$;
-
дизъюнктивная нормальная форма (ДНФ) -- дизъюнкция нескольких конъюнкций, например, $\left(A\wedge \overline{B}\wedge C\right)\vee \left(B\wedge C\right)$.
СКНФ
Совершенная конъюнктивная нормальная форма (СКНФ) -- это КНФ, удовлетворяющая трем условиям:
-
не содержит одинаковых элементарных дизъюнкций;
-
ни одна из дизъюнкций не содержит одинаковых переменных;
-
каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.
Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.
Правила построения СКНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.
СДНФ
Совершенная дизъюнктивная нормальная форма (СДНФ) -- это ДНФ, удовлетворяющая трем условиям:
-
не содержит одинаковых элементарных конъюнкций;
-
ни одна из конъюнкций не содержит одинаковых переменных;
-
каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.
Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.
Правила построения СДНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.
Примеры нахождения СКНФ и СДНФ
Записать логическую функцию по ее таблице истинности:
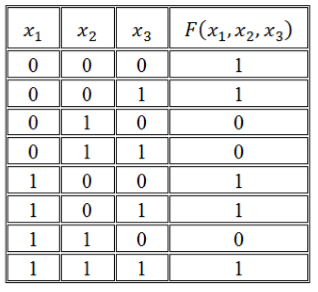
Рисунок 1.
Решение:
Воспользуемся правилом построения СДНФ:
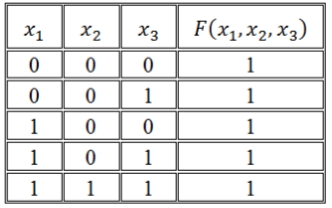
Рисунок 2.
Получим СДНФ:
\[F\left(x_1,\ x_2,\ x_3\right)=\left(\overline{x_1}\wedge \overline{x_2}\wedge \overline{x_3}\right)\vee \left(\overline{x_1}\wedge \overline{x_2}\wedge x_3\right)\vee \left(x_1\wedge \overline{x_2}\wedge \overline{x_3}\right)\vee \left(x_1\wedge \overline{x_2}\wedge x_3\right)\vee \left(x_1\wedge x_2\wedge x_3\right)\]Воспользуемся правилом построения СКНФ:
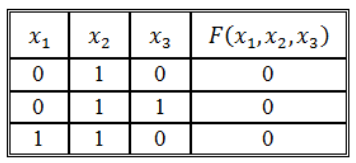
Рисунок 3.
Получим СКНФ:
\[F\left(x_1,\ x_2,\ x_3\right)=\left(x_1\vee \overline{x_2}\vee x_3\right)\wedge \left(x_1\vee \overline{x_2}\vee \overline{x_3}\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee x_3\right)\]Функция задана таблицей истинности:
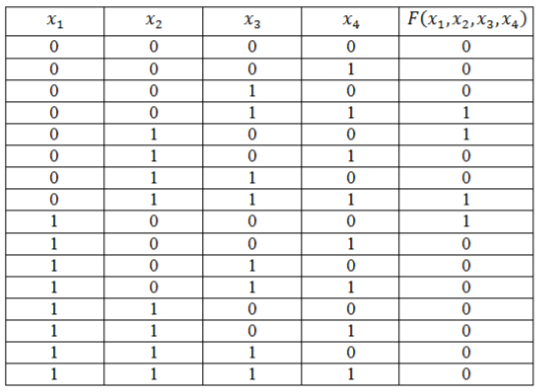
Рисунок 4.
Представить эту функцию в виде СДНФ и СКНФ.
Решение:
-
Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.
Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.
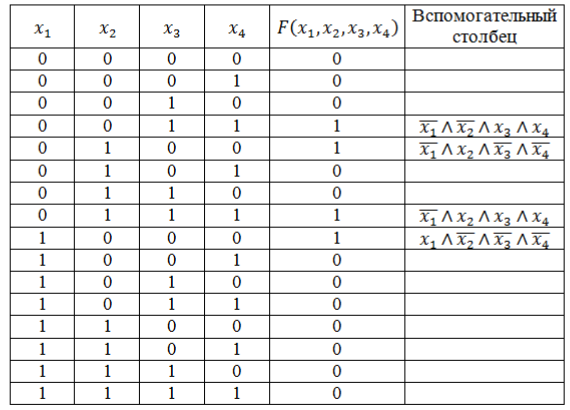
Рисунок 5.Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:
\[F\left(x_1,x_2,x_3,x_4\right)=\left(\overline{x}\wedge \overline{y}\wedge z\wedge f\right)\vee \left(\overline{x_1}\wedge x_2\wedge \overline{x_3}\wedge \overline{x_4}\right)\vee \left(\overline{x_1}\wedge x_2\wedge x_3\wedge x_4\right)\vee \left(x_1\wedge \overline{x_2}\wedge \overline{x_3}\wedge \overline{x_4}\right).\] -
Запишем логическую функцию в СКНФ.
Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.
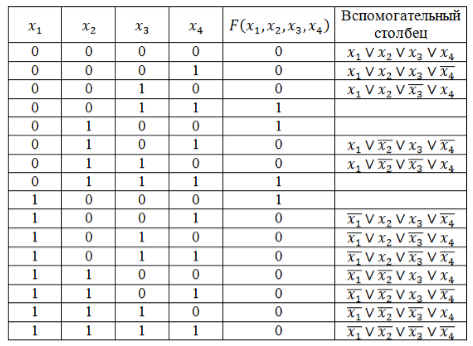
Рисунок 6.Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:
\[F\left(x_1,x_2,x_3,x_4\right)=\left(x_1\vee x_2\vee x_3\vee x_4\right)\wedge \left(x_1\vee x_2\vee x_3\vee \overline{x_4}\right)\wedge \left(x_1\vee x_2\vee \overline{x_3}\vee x_4\right)\wedge \left(x_1\vee \overline{x_2}\vee x_3\vee \overline{x_4}\right)\wedge \left(x_1\vee \overline{x_2}\vee \overline{x_3}\vee x_4\right)\wedge \left(\overline{x_1}\vee x_2\vee x_3\vee \overline{x_4}\right)\wedge \left(\overline{x_1}\vee x_2\vee \overline{x_3}\vee x_4\right)\wedge \left(\overline{x_1}\vee x_2\vee \overline{x_3}\vee \overline{x_4}\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee x_3\vee x_4\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee x_3\vee \overline{x_4}\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee \overline{x_3}\vee x_4\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee \overline{x_3}\vee \overline{x_4}\right).\]











