Логические переменные изучают в разделе математики, называемым алгеброй логики или алгеброй высказываний, или булевой алгеброй. В алгебре логики любое составное высказывание рассматривается как логическая функция $F(A, B, C, \dots )$, аргументы которой - логические переменные $A$, $B$, $C \dots$ (где $A$, $B$, $C$ -- являются простыми высказываниями). Логические функции $F(A, B, C, \dots )$ и логические переменные ($A$, $B$, $C$ - аргументы) могут принимать только два значения: «истина» ($1$) или «ложь» ($0$). Логическую функцию часто называют предикатом.
Логической (булевой) функцией называют функцию $F(X_1, X_2, ..., X_n)$, аргументы которой $X_1, X_2, ..., X_n$ (независимые переменные) и сама функция (зависимая переменная) принимают значения $0$ или $1$.
Таблицу, показывающую, какие значения принимает логическая функция при всех сочетаниях значений ее аргументов, называют таблицей истинности логической функции.
Таблица истинности логической функции от n аргументов содержит $2_n$ строк, $n$ столбцов значений аргументов и $1$ столбец значений функции.
Логическая функция может быть задана аналитическим (при помощи формул) или табличным способом.
Логическая функция, представленная с помощью инверсии, дизъюнкции и конъюнкции называется нормальной.
Всего существует $16$ различных логических функций от двух переменных. Переменные образуют четыре пары значений: $(1, 1), (1, 0), (0,0), (0,1)$, а количество функций, которые возможно описать равно $24 = 16$.
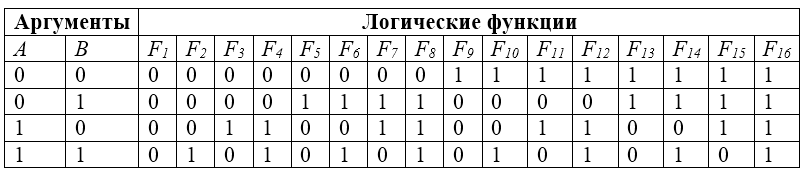
Рисунок 1. Логические функции двух переменных
Общепринятые названия функций $F_1 \dots F_16$
Функция $F_1 = 0$ - функция генератора $0$.
Функция $F_2 = A \& B$ - функция конъюнкции.
Функция $F_3 = A \& \bar{B}$- функция запрета по логической переменной $A$.
Функция $F_4 = A$ - функция повторения по логической переменной $A$.
Функция $F_5 = \bar{A} \& B$ - функция запрета по логической переменной $B$.
Функция $F_6 = B$ - функция повторения по логической переменной $B$.
Функция $F_7 = \bar{A} \& B \vee A \& \bar{B}$ - функция исключающее «ИЛИ».
Функция $F_8 = A \vee B$ - функция дизъюнкции.
Функция $F_9 = \bar{A \vee B}$ - функция Пирса.
Функция $F_{10} = A \& B \bar{A} \& \bar{B}$ - функция эквивалентности.
Функция $F_{11} = \bar{B}$ - функция инверсии (отрицания) логической переменной $B$.
Функция $F_{12} =B\to A$ - функция импликации $B\to A$.
Функция $F_{13} = \bar{A}$ - функция инверсии (отрицания) логической переменной $A$.
Функция $F_{14} =A\to B$ - функция импликации $A\to B$.
Функция $F_{15} = A \& B$ - функция Шеффера.
Функция $F_{16} = 1$ - функция генератора $1$.
Среди перечисленных выше шестнадцати логических функций от двух переменных можно выделить такие логические функции, с помощью которых выражаются другие логические функции. Операция замены одной логической функции на другую в алгебре логики (булевой алгебре) называется операцией суперпозиции или метод суперпозиции.
Функцию Шеффера методом суперпозиции можно выразить при помощи функций отрицания и дизъюнкции, используя закон Де Моргана:
$F_{15} = \bar{A \& B} = \bar{A} \vee \bar{B}$
Наиболее широко в качестве базовых функций используют три логических функции: конъюнкцию, дизъюнкцию и отрицание. В приведенном примере логическая функция Шеффера выражена через базовые функции и представлена в нормальной форме.
Каждой базовой функции соответствует техническое устройство, реализующее эту логическую функцию.
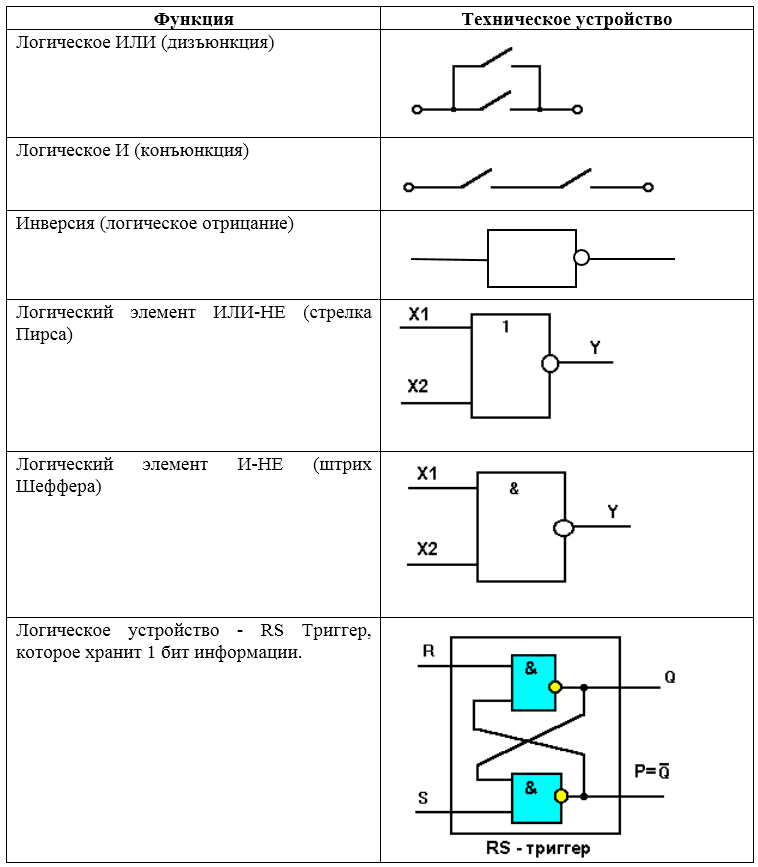
Рисунок 2. Соответствие базовой функции и технического устройства
Наборы И-НЕ и ИЛИ-НЕ являются функционально полными или базисными наборами.
При помощи набора базовых функций и соответствующих им технических устройств, которые реализуют эти логические функции, создаются любые логические устройства или системы.
Логическое устройство имеет сколь угодное количество входов и только один выход (См. рис.3).
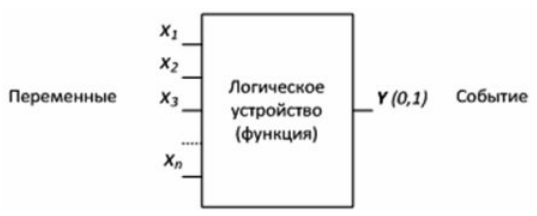
Рисунок 3. Схематичное представление логического устройства
Отдельные логические устройства от $x_1 \dots x_n$ переменных схематично представлены на рисунке 4.
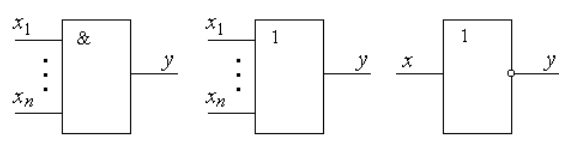логических элементов на электрических схемах: И (а), ИЛИ (б), НЕ (в)">
Рисунок 4. Условное обозначение логических элементов на электрических схемах: И (а), ИЛИ (б), НЕ (в)
Приведем пример реализации функции при помощи инверсии и отрицания (в базисе И-НЕ).
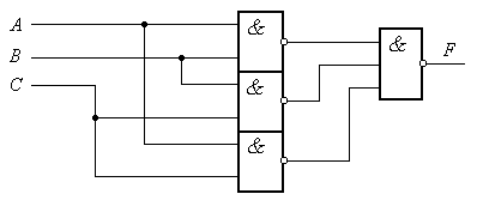
Рисунок 5. Пример реализации функции $F = AB \vee BC \vee AC$ в базисе И-НЕ
Построим схему охранной сигнализации на простых логических элементах. Генератор Г вырабатывает сигнал сирены, подавая его на усилительный каскад через логический элемент «И» на микросхеме $DD2$. Если замкнуты ключи $S1 - S4$, то на входы элемента $DD1$ подается $«0»$ - на нижний вход элемента «И» $DD2$ тоже $«0»$, на затворе транзистора $VT$ будет тоже $«0»$. Если хотя бы один из ключей разомкнут, то на вход элемента $DD1$ через резистор $R_i$ поступит напряжение или $«1»$, что даст возможность сигналу с генератора Г попасть на затвор транзистора, к которому подключен динамик.
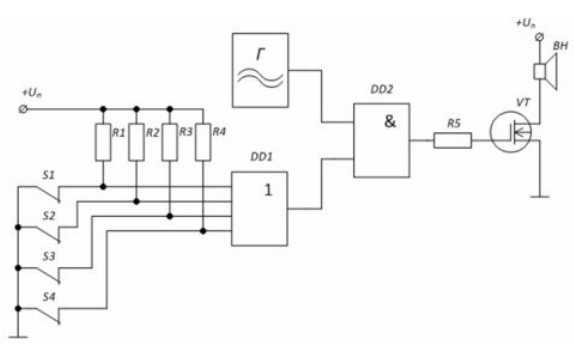
Рисунок 6. Пример схемы охранной сигнализации
