Понятие системы массового обслуживания
В человеческой жизнедеятельности огромное значение имеют процессы массового обслуживания, возникающие в системах, которые предназначены для многоразового использования при решении однотипных задач. Подобные системы называют системами массового обслуживания (СМО). Например, телефонные системы, вычислительные комплексы, системы ремонтного обслуживания, автотранспортного, авиационного соединения, системы магазинов, билетные кассы и т.д.
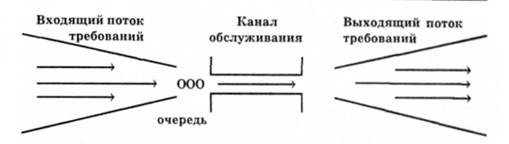
Каждая система включает определенное количество единиц, которые обслуживают ее работу – приборы, аппараты, устройства, станции и т.д. Такие единица называют каналами обслуживания. По количеству каналов СМО делятся на одноканальные и многоканальные.
Заявки в систему поступают зачастую не регулярно, а случайно, тем самым образуют случайный поток заявок. Обслуживание каждой заявки занимает определенное время, но чаще – неопределенное. Случайный характер приводит неравномерной загруженности СМО: в одни периоды времени накапливается огромное число заявок (они могут становиться в очередь или покидать СМО не обслуженными), в другие периоды СМО может простаивать или работать с недогрузкой.
Исследование систем массового обслуживания проводится с целью анализа качества их функционирования и выявления возможностей его улучшения. При этом качество функционирования в отдельных случаях будет иметь свое значение и выражается разными количественными показателями. Например, величиной очереди на обслуживание, средним временем обслуживания, ожиданием обслуживания или нахождения заказа в обслуживающей системе, временем простоя обслуживающих аппаратов; уверенностью, что все поступившие в систему заказы будут обслужены.
Следовательно, качество функционирования СМО – это не само качество выполнения определенной работы, запрос на которую поступил, а степень удовлетворения потребности в обслуживании.
Для развития эффективности систем массового обслуживания строят математические модели, которые связывают заданные условия работы СМО (число каналов, их производительность, характер потока заявок и т.п.) с показателями ее эффективности, которые описывают ее способность справляться с потоком заявок.
Методы исследования СМО
Для исследования процессов СМО используется два метода:
- аналитический;
- метод статистического моделирования (метод Монте-Карло).
На практике СМО далеки от упрощенных систем. Например, поток событий часто может оказаться не простейшим, а время обслуживания в реальных системах может носить любой характер распределения. При помощи метода статистического моделирования случайных процессов (метода Монте-Карло) могут быть успешно решены многие самые сложные задачи (особенно которые возникают в производственных системах).
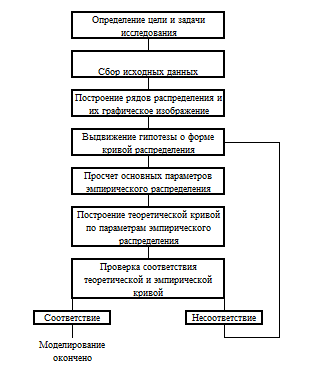
Этапы построения математической модели Монте-Карло:
- Сформировать цели задачи и выбрать ограничительные условия функционирования СМО.
- Провести наблюдения за ходом производства, т.е. получить исходные данные.
- Выполнить первичную обработку данных, построить ряды распределения и их графический анализ. Выдвинуть гипотезу о характере закона распределения.
- Построить теоретическое распределение с параметрами данных эмпирического наблюдения.
- Проверить соответствие теоретического и эмпирического распределения.
Для наблюдения заходом производственного процесса используют данные хронометража, фотографий, журнала регистрации простоев оборудования, данные автоматизированных информационных систем (АИС) и другие методы получения информации.
После построения математической модели производственного процесса проводят случайные испытания и моделируют на их основе ход производственного процесса. Случайные испытания проводят чаще всего на основе равновероятного распределения, от которого переходят к распределению, описывающегося математической моделью. Далее строится график производственного процесса на основе случайных испытаний. Для проведения случайных испытаний используют различные методы, среди которых метод жеребьевки: случайный отбор по схеме повторного отбора (шары из урны), моделирование случайных испытаний с помощью компьютера, использование таблиц случайных чисел.
Задачи, которые решаются методами теории массового обслуживания
- Расчет количества вспомогательных рабочих (расчет норм обслуживания): наладчиков, электриков, дежурных слесарей.
- Расчет необходимого количества кранов.
- Определение страховых заделов.
- Определение страховых запасов.
- Расчет необходимой площади материальных складов.