Принцип линейности свободных энергий
Уравнение Гаммета проводит линейную зависимость между константами скоростей и равновесий химических реакций и тем самым указывает на линейную связь между свободными энергиями этих процессов.
Уравнение Гаммета $lgk_{ij}-lgk_{0j}={\rho }_j{\sigma }_i$ отражает принцип линейности свободных энергий.
Рассмотрим две реакции $A$ и $B$, между которыми наблюдается линейное соотношение свободных энергий. В реагентах есть заместители $X, Y, Z$ (Рис.1).
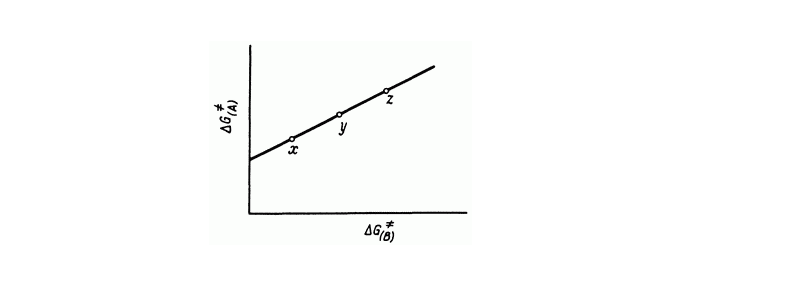
Рисунок 1. Линейное соотношение свободных энергий для двух реакций
Представленный график можно описать уравнением
\[\triangle G^{\ne }_{\left(A\right)}=\alpha \triangle G^{\ne }_{\left(B\right)}+const.\]Для выполнения этого соотношения необходимы некоторые допущения:
-
Свободные энергии реакций включают два члена и только один из них зависит от заместителя. Если за стандартное уравнение изменения свободной энергии взять уравнение для реакции $A$ с $X$-замещенным реагентом,
\[\triangle G^{\ne }_{\left(A\right)Х}=\triangle G^{\ne }_{\left(A\right)0,}\]то для реакции Y-замещенного реагента изменение свободной энергии имеет вид
\[\triangle G^{\ne }_{\left(A\right)Y}=\triangle G^{\ne }_{\left(A\right)0}+{\delta G}^{\ne }_{\left(A\right)Y}\]для $Z$-замещенного реагента
\[\triangle G^{\ne }_{\left(A\right)Z}=\triangle G^{\ne }_{\left(A\right)0}+{\delta G}^{\ne }_{\left(A\right)Z.}\]В общем виде для заместителя~S
\[\triangle G^{\ne }_{\left(A\right)S}=\triangle G^{\ne }_{\left(A\right)0}+{\delta G}^{\ne }_{\left(A\right)S.}\]Аналогично для реакции $B$
\[\triangle G^{\ne }_{\left(B\right)S}=\triangle G^{\ne }_{\left(B\right)0}+{\delta G}^{\ne }_{\left(B\right)S.}\] -
Зависимые от заместителей, вклады членов ${\delta G}^{\ne }_{\left(A\right)S}$ и ${\delta G}^{\ne }_{\left(B\right)S}$ меняются линейно:
\[{\delta G}^{\ne }_{\left(A\right)S}={\alpha \delta G}^{\ne }_{\left(B\right)S}\]Выполнив ряд подстановок и замещений, получаем зависимость
\[\triangle G^{\ne }_{\left(A\right)S}={\alpha \triangle G}^{\ne }_{\left(B\right)S}+\left(\triangle G^{\ne }_{\left(A\right)0}-\alpha \triangle G^{\ne }_{\left(B\right)0}\right)\]Найдем для реакций $A$ и $B$ разность свободных энергий $\triangle \triangle G^{\ne }$ с $Y$- и $Z$-замещенными реагентами. Вычитание двух уравнений, где $S$ является $Y$ и $Z$ соответственно дает соотношение
\[{\triangle }_{Y-Z}\triangle G^{\ne }_{\left(A\right)}=\alpha \left({\triangle }_{Y-Z}\triangle G^{\ne }_{\left(B\right)}\right)\]Соотношение констант равновесия (скорости) можно привести к виду
\[ln\left(\frac{k_{AZ}}{k_{AY}}\right)=\alpha ln\left(\frac{k_{BZ}}{k_{BY}}\right),\]где $k_{AZ}$ -- константа равновесия или скорости реакции $A$ для $Z$-замещенного реагента и т.д. аналогично для других реакций.
\[lnk_{AZ}=\alpha lnk_{BZ}+const\]
Уравнение Бренстеда как форма выражения принципа линейности свободных энергий
Уравнение Бренстеда для катализируемых кислотой реакций можно вывести из уравнения $lnk_{AZ}=\alpha lnk_{BZ}+const,$
если $k_{AZ}$- константа скорости реакции $(kc)$;
$k_{BZ}$- константа ионизации кислоты $(HA).$
Уравнение Бренстеда показывает корреляцию между двумя реакциями с переносом протона от кислоты $HA$ к субстрату $S$ (эффект по $kc$) и к воде (эффект по$K_{HA}$).
Коэффициент Бренстеда $\alpha $ связан с разницей свободных энергий сольватации катионов $HS^+$ и $H_3O^+$. Так как свободная энергия гидратации $H_3O^+$ велика, Коэффициент Бренстеда должен быть больше единицы. Экспериментально установлено, что его значение лежит в пределах от $0,3$ до $0,9$.
Постулат Хэммонда
Если переходное состояние и промежуточный комплекс имеют практически одинаковую энергию, то их взаимопревращения содержат небольшие изменения структуры.
Согласно Хэммонду, переходное состояние, включающее две или несколько реагирующих частиц (ионов, молекул, свободных радикалов) имеет такое графическое изображение, при котором максимум энергии соответствует вершине горба в координатах системы: энергия системы (ордината) -- координата реакции (абсцисса).
Хэммонд считал, что если переходное состояние ведет к неустойчивому интермедиату, то это состояние имеет схожую с интермедиатом энергию. При этом, переход между двумя состояниями может быть осуществлен за счет небольшого изменения структуры молекулы.
Если же процесс ведет к продукту, который более устойчив, чем, субстрат, то переходное состояние энергетически и структурно будет ближе неустойчивому субстрату.
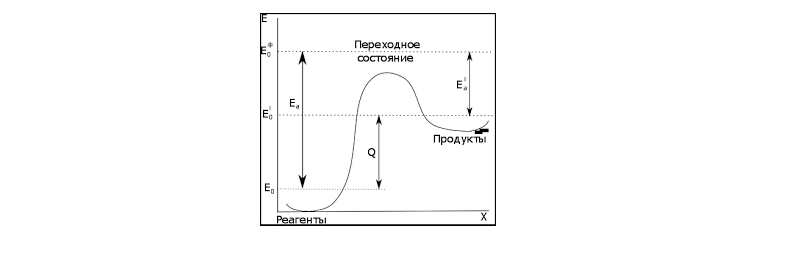
Рисунок 2.
Иными словами, структура переходного состояния энергетически может быть близка как к субстрату, так и к продукту. Если реакция экзотермическая -- переходное состояние ближе к реагенту, если эндотермическая -- к продукту реакции.
Таким образом, экзотермическая реакция имеет низкую энтальпию активации, а эндотермическая -- высокую энтальпию активации.
Постулат Хэммонда показывает, что при изменении скорости реакции обязательно происходит изменение структуры переходного состояния.












