Предпосылки вывода уравнения Шредингера
Основная идея волновой механики заключается в том, что для таких малых тел, как электрон, нельзя с определенностью сказать, где оно находится в данное время и куда направляется. Можно установить только относительную вероятность его нахождения в том или ином месте и наличие определенного количества движения в определенный момент времени.
В соответствии с волновой механикой какая-либо система – атом, молекула, электрон и т.д. – описывается функцией состояния или волновой функцией, обозначаемой $\psi$ («пси»), которая является функцией координат всех частиц, образующих эту систему. Следовательно, величина $\psi$ зависит только от положения всех частиц в пространстве.
В 1924 г. де Бройль предположил, что точно также, как свет, который, как обычно считают, имеет волновую природу, на самом деле при определенных обстоятельствах ведет себя, как будто он состоит из частиц – квантов, - так и очень малые частицы, такие, как электроны, также могут обладать волновыми свойствами. Де Бройль предположил, что с пучком электронов следует связывать длину волны, определяемую уравнением
$\lambda =\frac{\hbar }{p} $ (1)
где $\hbar$ – постоянная Планка ($6,626\cdot 1034 Дж\cdot с$ или $6,626\cdot 10-27 эрг\cdot с$), а $p$ – количество движения (импульс) электрона в пучке, т.е. его масса, умноженная на его скорость.
Физическое подтверждение волновой природы электрона было продемонстрировано в 1927 – 1928 гг. Дейвиссоном, Джермером и Томсоном, которые показали, что пучок электронов может испытывать дифракцию на подходящей решетке (атомы в кристалле золота), аналогичную дифракции пучка света.
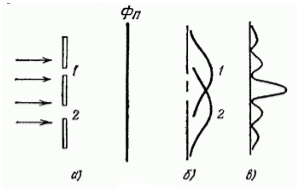
Рисунок 1. Дифракция пучка электронов
На преграду с двумя узкими щелями направлен параллельный пучок моноэнергетических (т.е. обладающих одинаковой кинетической энергией) электронов (рис. 1. а). За преградой находится фотопластина $Фn$. При закрытии щели номер $2$ и экспонировании в течение времени $t$ почернение на проявленной фотопластине будет характеризоваться кривой $1$ (рис. 1. б). При закрытии щели номер $1$, соответственно, почернение на фотопластине будет соответствовать кривой $2$. Однако в случае, когда открыты обе щели картина почернения фотопластины (рис. 1. в) отнюдь не эквивалентна наложению двух первых картин. Зато она аналогична картине, получающейся при интерференции двух когерентных световых волн.
Тот факт, что системы малых частиц проявляют, по крайней мере, при определенных условиях, волновые свойства, предполагает возможность описания таких систем уравнениями, подобными те, которые описывают другие виды волнового движения, например, волны, которые распространяются вдоль колеблющейся струны, или волновое движение, приписываемое электромагнитному излучению. Действительно, можно начать с волнового уравнения, соответствующего электромагнитным волнам, и путем определенных замен, превратить его в уравнение, соответствующее нашему случаю. Хотя эти замены диктуются физическими причинами, они в основном произвольны и могут быть приняты только потому, что приводят к уравнению, которое, как показывает опыт, позволяет получить правильное решение физических задач. Поэтому следует принять волновое уравнение как постулат, так как у химиков основной интерес вызывает применение волнового уравнения к атомным и молекулярным системам, а не физические и математические соображения, которыми руководствовался Шредингер, впервые его предложивший в 1925 г.
Общий вид уравнения Шредингера

Рисунок 2. Эрвин Шрёдингер (1887 - 1961)
Волновое уравнение, применяемое для расчета стационарных состояний системы, можно записать в символическом виде:
${\mathcal H}\psi =E\psi $ (1)
где $H$ представляет собой определенный способ выражения общей энергии системы, а $E$ – числовое значение этой энергии. Для всех систем, которые обычно интересуют химиков, общая энергия представляет собой сумму кинетической энергии $Т$ и потенциальной энергии $V$:
$H=T+V$ (2)
Это соотношение было широко использовано физиком-теоретиком Гамильтоном, поэтому $H$ часто называют функцией Гамильтона, а $\mathcal H$ гамильтонианом системы.
Уравнение Шредингера на примере атома водорода
Рассмотрим модель атома водорода, предложенную Бором. Для простоты предположим, что тяжелое ядро закреплено (оно почти, но не совершенно неподвижно, когда электрон движется вокруг него). Тогда полная кинетическая энергия $Т$ системы представляет собой просто кинетическую энергию электрона
$T=\frac{1}{2} mv^{2} $ (3)
где $m$ – масса электрона и $\nu$ – его скорость. Потенциальная энергия системы есть просто энергия, возникающая вследствие электростатического взаимодействия (гравитационные силы приблизительно в $10^{18}$ раз меньше), и ее можно выразить как
$V=-\frac{e^{2} }{r} $ (4)
где $e$ - заряд электрона, $r$ - радиус орбиты, знак минус появляется вследствие того, что заряд одной из частиц положителен $(+)$, а другой отрицателен $(-)$. Поэтому для атома водорода функция Гамильтона в классической (т.е. доквантовомеханической) физике равна:
$H=\frac{1}{2} mv^{2} -\frac{e^{2} }{r} $ (5)
Если использовать понятие количества движения электрона $p=m\nu$, данное уравнение запишется в следующем виде:
$H=\frac{p^{2} }{2m} -\frac{e^{2} }{r} $ (6)
Теперь для перехода от классического описания этой или какой-либо другой системы к описанию при помощи волновой механики, необходимо взять функцию Гамильтона (уравнение 6) и произвести в ней определенные замены: в функции Гамильтона количество движения следует заменить выражением
$\frac{\hbar }{2\pi } \left(\frac{\partial }{\partial x} +\frac{\partial }{\partial y} +\frac{\partial }{\partial z} \right)$ (7)
Таким образом, гамильтониан для атома водорода в его квантовомеханической форме ${\mathcal H}$ следует записать в виде
${\mathcal H}=-\frac{{\hbar }^2}{8{\pi }^2m}\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}\right)-\frac{e^2}{r}$ (8)
Если теперь это выражение гамильтониана подставить в общее волновое уравнение (уравнение 1), то получим:
${\mathcal H}\psi =\left[-\frac{{\hbar }^2}{8{\pi }^2m}\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}\right)-\frac{e^2}{r}\right]\psi =E\psi $ (9)
Это и есть волновое уравнение для атома водорода. Из уравнения 9 следует, что нужно вторые производные функции $\psi $ сложить и умножить на $-{{\hbar }^2}/{8{\pi }^2m}$, затем к этому добавить $\left(-{e^2}/{r}\right)\psi $, тогда получим величину, тождественную Е$\psi $. Если найдена функция $\psi $, то говорят, что она является решением волнового уравнения, и ее называют волновой функцией. Вообще, может быть несколько различных функций $\psi_1$, $\psi_2$, ... , $\psi_n$, которые являются решениями уравнения 9, причем каждой соответствует свое значение энергии $Е_1$, $Е_2$, ... , $Е_n$.












