Химическая связь, возникающая в результате взаимодействия электронов и ядер, может быть математически описана только в рамках квантовой механики. Это описание весьма сложно, так как имеются большие трудности при решении соответствующих уравнений.
Поиски приближенных методов решения таких уравнений для молекулярных систем являются одной из задач квантовой химии.
В настоящее время в квантовой химии используются два приближенных метода расчета молекул: метод валентных связей и метод молекулярных орбиталей.
В методе валентных связей предполагается, что образование молекулы происходит при сближении между собой целых атомов, которые и в молекуле в некоторой мере сохраняют свою индивидуальность. При этом истинное состояние молекулы представляется как наложение (суперпозиция) не существующих в действительности крайних гомеополяриых или ионных структур.
При решении задач методом молекулярных орбиталей предполагается, что при образовании химической связи сначала сближаются только ядра и лишь затем на образующихся многоцентровых молекулярных орбиталях размещаются валентные электроны, причем при расчете молекулярных орбиталей используется тот же подход, что и при расчете атомных орбиталей.
В обычных самых простых расчетах (нулевое приближение) предполагают, что молекулярная орбитальная функции является линейной комбинацией атомных орбитальных функций (приближение ЛКАО).
Оба рассматриваемых метода весьма неточны. Однако с их помощью могут быть оценены важные дли химиков величины: энергия, устойчивость различных форм молекулы, порядок связи, индексы свободной (неиспользованной) валентности на отдельных атомах, распределение зарядов в молекуле.
Все эти данные полезны при объяснении характерных особенностей реакционной способности органических соединений. Однако следует иметь в виду, что особенности стационарного состояния молекул далеко не всегда определяют их реакционную способность: решающую роль может играть «выгодность» или «невыгодность» тех или иных переходных состояний.
С появлением вычислительных машин, во-первых, значительно упростились простые расчеты и, во-вторых, оказалось возможным увеличить приближение.
Результаты таких расчетов используются в некоторых случаях при последующем изложении фактического материала.
Понятие о квантовомеханических расчетах и реакционных индексах
Ранее приводилось волновое уравнение Шредингера и сведения о его применении для приближенного расчета электронных орбиталей ($1s$, $2s$, $2р$) простейших атомов. Для многоэлектронных атомов волновое уравнение точно решить невозможно. Еще более сложны подобные задачи в случае молекулярных орбиталей. Тем не менее разработаны крайне упрощенные приближенные методы расчета молекулярных орбиталей ($MO$). К числу этих методов определения $MO$ относится метод линейных комбинаций атомных орбиталей (ЛК АО), впервые предложенный Хундом. В основе метода лежит допущение, что при наличии на молекулярной орбитали молекулы $A-B$ двух электронов каждый электрон, проходя вблизи ядра атома $A$ следует по соответствующей орбитали $A$, точно так же каждый электрон, находясь в сфере атома $B$, следует по орбитале с функцией $\psi B$ Таким образом, функция молекулярной орбитали получается из «линейного сочетания атомных орбиталей»:
$\psi AB= CA \psi A+ CB \psi B$
где $CA$ и $CB$ - переменные параметры, выбираемые таким образом, чтобы энергия, вычисляемая из функции $\psi AB$, имела наименьшую величину.
Для молекулы водорода $Н_2$ математическая обработка приводит к двум решениям, выражающим два различных - низкое и высокое - энергетических состояния молекулы. Первое соответствует связывающей молекулярной орбитали, второе - разрыхляющей орбитали.
Практически электроны находятся лишь на связывающей орбитали.
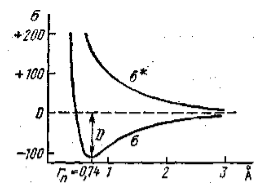
Рисунок 1. Кривые потенциальной энергии, отнесенные к расстоянию между двумя атомами водорода
Для кривой $\sigma $ (приводящей к образованию связывающей орбитали) вначале с уменьшением расстояния между атомами ($3-2-1 \dot{A}$) энергия системы постепенно уменьшается. На расстоянии $0,74 \dot{A}$, соответствующем межатомному расстоянию в $H_2$ в основном состоянии молекулы, энергия минимальна. Именно это и характеризует образование молекулы из атомов, т. е. образование связывающей орбитали. Верхняя кривая $\sigma $* на всем протяжении обладает большей энергией, чем нижняя, и не имеет минимума, атомы не связываются.
Другой метод расчета $MO$ - метод валентных пар. Оба метода, усовершенствованные Хюккелем, дают близкие конечные результаты расчетов.
В каждой науке наиболее ценны методы и приемы, дающие возможность не только объяснить, но и предсказать явления, особенно с количественной стороны. В этом отношении квантовая химия приобретает особое значение, так как во многих случаях дает возможность количественно характеризовать реакционную способность соединений. Наибольшей реакционной способностью обладают соединения с кратными связями, т. е. содержащиеся связи. В упрощенных квантовомеханических расчетах оказалось возможным, пренебрегая взаимодействием $\sigma $- и $\pi $- электронов, охарактеризовать реакционную способность на основании определения молекулярных орбиталей, энергии и зарядов на атомах исходя из соответствующих величин только для $z$- электронов.
Реакционные индексы
Подобные полуэмпирические методы дали возможность вычислить так называемые реакционные индексы, характеризующие электронное строение и дающие представление о реакционной способности молекул. К ним относятся: порядок связи, индекс свободной валентности, $\pi $-электронная плотность, энергия делокализации электронов и некоторые другие.
1. Порядок связи ($P$). Поскольку электроны весьма подвижны, особенно на я-орбиталях, далеко не во всех случаях связи образованы парой электронов или двумя (тремя) парами, т. е. не всегда приходится иметь дело с типичными одинарными, двойными и тройными связями. Эго имеет место, в частности, в диеновых системах с сопряженными связями. В таких системах нет истинных двойных и одинарных, связей. Порядок связи в таких случаях выражается цифрами, например $1,8942$ для связи $C(1)-C(2)$, что свидетельствует, что менее двух пар электронов, а именно $1,8942$ электронной пары, соединяет эти атомы. Остальная часть электронов перемещается к связи $C(2)-C(3)$.
-
Индекс свободной валентности. Этот индекс характеризует меры ненасыщенности того или иного атома в молекуле, его способность к присоединению.
-
Электронная плотность. Величина выражает распределение зарядов между атомами молекул, что указывает, какой из атомов наиболее легко будет вступать в реакцию с положительно или отрицательно заряженными частицами (неорганическими или отрицательно заряженными ионами или полярными группами).
-
Энергия делокализации (ЭД). Так как одним из основных принципов квантовой механики является принцип неопределенности, все электроны не локализуются на какой-либо определенной линейной орбите, они делокализованы. Делокализация электронов стабилизирует молекулу. Однако степень делокализации неодинакова. Энергия, характеризующая степень делокализации, называется энергией делокализации; в известной степени она характеризует устойчивость молекулы.












