В этой статье мы рассмотрим понятие подобных треугольников и другие понятия и теоремы, связанные с этим определением.
Определение подобных треугольников
Будем рассматривать следующие два треугольника (Рис. 1).
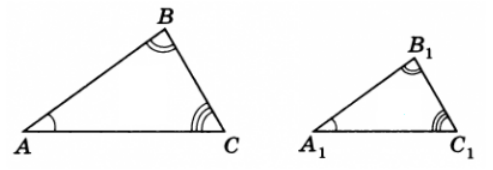
Рисунок 1. Подобные треугольники
Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны, то есть
\[\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1,\] \[\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}\]Обозначение: $ABC\sim A_1B_1C_1$
Число $k$, равное отношению сходственных сторон подобных фигур называется коэффициентом подобия этих фигур.
Соотношение площадей подобных треугольников
С этим понятием связана следующая теорема о соотношении площадей подобных треугольников. Рассмотрим её без доказательства.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия, то есть
\[\frac{S_{ABC}}{S_{A_1B_1C_1}}=k^2\]Признаки подобия треугольников
Приведем формулировки трех признаков подобия треугольников.
Первый признак подобия треугольников: Если два угла одного треугольника соответственно равны двум углам второго треугольника, то такие треугольники подобны.
То есть, если $\angle A=\angle A_1,\ \angle B=\angle B_1$, то треугольники $ABC$ и $A_1B_1C_1$ подобны (рис. 2).
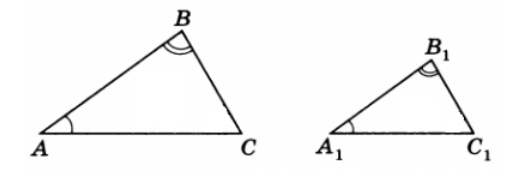
Рисунок 2. Первый признак подобия треугольников
Второй признак равенства треугольников: Если две стороны одного треугольника пропорциональны соответствующим сторонам второго треугольника и углы между этими сторонами равны, то данные треугольники подобны.
То есть, если $\angle A=\angle A_1$ и $\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}$, то треугольники $ABC$ и $A_1B_1C_1$ подобны (рис. 3).
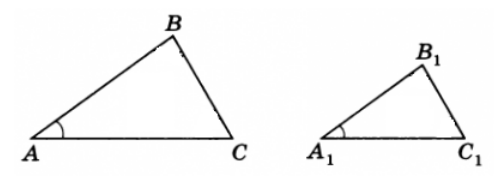
Рисунок 3. Второй признак подобия треугольников
Третий признак подобия треугольников: Если три стороны одного треугольника пропорциональны трем соответствующим сторонам второго треугольника, то такие треугольники подобны.
То есть, если $\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}$, то треугольники $ABC$ и $A_1B_1C_1$ подобны.
Примеры задач на понятие подобия треугольников
Подобны ли равнобедренные треугольники, если они имеют
-
По равному острому углу;
-
По равному тупому углу;
-
По равному прямому углу.
Решение.
Пусть даны равнобедренные треугольники $ABC$ и $A_1B_1C_1$ с $\angle A=\angle A_1.$
-
Пусть $\angle A=\angle A_1$ -- острые углы треугольников. Тогда здесь возможны два случая:
а) $\angle A=\angle A_1$ - углы при вершине данных треугольников. Тогда, так как треугольник $ABC$ равнобедренный, то
\[\angle B=\angle C=\frac{180-\angle A}{2}\]Так как треугольник $A_1B_1C_1$ равнобедренный, то
\[\angle B_1=\angle C_1=\frac{180-A_1}{2}=\frac{180-\angle A}{2}=\angle B=\angle C\]То есть $\angle B=\angle B_1,\ \ \angle C=\angle C_1$. По первому признаку подобия, получаем, что треугольники $ABC$ и $A_1B_1C_1$ подобны.
б) $\angle A=\angle A_1$ - углы при основании данных треугольников. Так как треугольники подобны, то их углы при основании равны. Но тогда два соответствующих угла одного треугольника равны двум соответствующим углам второго треугольника. Значит, по первому признаку подобия треугольников, треугольники подобны.
-
Так как угол тупой, то он лежит при основании данных треугольников. Аналогично пункту 1,а) получим, что они подобны.
-
Так как угол прямой, то он лежит при основании данных треугольников. Аналогично пункту 1,а) получим, что они подобны.
Подобны ли треугольники $ABC$ и $A_1B_1C_1$, если $AB=17,\ BC=30,\ \ AC=42,\ {\ A}_1B_1=34,\ {\ B}_1C_1=60,\ \ A_1C_1=84$?
Решение.
Найдем коэффициент подобия каждой пары сторон треугольников:
\[\frac{AB}{A_1B_1}=\frac{17}{34}=\frac{1}{2}\] \[\frac{BC}{{B_1C}_1}=\frac{30}{60}=\frac{1}{2}\] \[\frac{AC}{A_1C_1}=\frac{42}{84}=\frac{1}{2}\]Получаем
\[\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}=\frac{1}{2}\]Следовательно, по третьему признаку подобия треугольников получаем, что данные треугольники подобны.











