Почему система уравнений Максвелла требует дополнения законом сохранения энергии?
Система уравнений Максвелла получает определенное физическое содержание только тогда, когда имеется указание в каких явлениях можно наблюдать и эмпирически исследовать электромагнитное поле. Дело в том, что человек не может непосредственно воспринимать это поле (исключение составляют световые волны). Мы можем определить, течет ли ток в проводнике лишь по тепловым эффектам (нагрев проводника) или механическим проявлениям (отклонение стрелки амперметра). То есть мы можем заключить о наличии электромагнитного поля только по появлению, при определенных условиях, доступных форм энергии, доступных нашему восприятию. Ориентируясь на принцип сохранения энергии, можно сделать вывод о том, что возникновение или исчезновение известных нам форм энергии может происходить за счет преобразования некоторой иной формы энергии, которую называют энергией электромагнитного поля $(W)$.
Итак, получается, что введение энергии электромагнитного поля в виде:
в теорию Максвелла система соответствующих уравнений станет доступной к проверке экспериментально. Это происходит потому, что уравнения максвелловской системы определяют, каким образом изменяется электромагнитное поле со временем, а уравнение (1) дает возможность выяснить, в каких преобразованиях эти изменения выявляются.
Энергия электромагнитного поля
Найдем энергию ($\triangle W$), которую переносит электромагнитная волна через произвольную площадку $S$ (рис.1), которая находится в поле волны за небольшой промежуток времени $\triangle t$. Выстроим параллелепипед на основании площадки $S$, причем ребра параллелепипеда сделаем параллельными скорости распространения волны ($\overrightarrow{v}$) и равными $v\triangle t.$ В таком случае объем данного параллелепипеда равен:
где $\alpha $ - угол между нормалью $\overrightarrow{n}$ к площадке $S$ и направлением вектора скорости (рис.1).
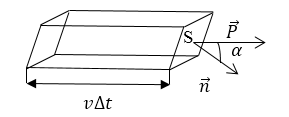
Рисунок 1.
В том случае, если обозначить через $u$ энергию единицы объема поля (объемную плотность энергии), то получим:
При этом объемна плотность энергии электромагнитной волны - есть сумма энергии электрического поля и энергии магнитного поля:
Так как напряженности в электромагнитной волне связаны выражением:
следовательно, можно записать, что:
Учтем, что:
тогда выражение (3) можно переписать в виде:
Получаем, что энергия, проходящая через площадку $S$ в единицу времени может быть представлена как:
где $P_n$- проекция вектора Умова - Пойнтинга на направление нормали.
Закон сохранения энергии
Пусть вещество, в котором существует электромагнитное поле неподвижно. При изменении электромагнитного поля и течении тока в единице объема совершается элементарная работа ($\delta A^{vnesh}$), равная:
Выражение (10) рассматривается как постулат макроскопической теории электричества.
Работа $\delta A^{vnesh}$ расходуется на изменение внутренней энергии, минус теплота, которая уходит из единицы объема в результате теплопроводности (в принципе, можно допустить, что она равна нулю). Если в данном случае, под $u$ понимать плотность всей внутренней энергии, а не только ее электромагнитной части, то:
выражение (11) - закон сохранения энергии в электродинамики (теорема Умова - Пойнтинга). В интегральном виде закон сохранения энергии в электродинамике имеет вид:
где $V$ - произвольный объем, который ограничен замкнутой поверхностью $S$.
Задание: Вдоль цилиндрического провода радиусом r течет постоянный ток силы $I$. Покажите, что электромагнитная энергия, которая будет связана с проводником с током, будет выделяться на данном проводнике как тепло Джоуля.
Решение:
Магнитное поля провода с током $(H)$ обвивается вокруг провода на поверхности проводника оно равно:
\[H=\frac{I}{2\pi r}=\frac{j\pi r^2}{2\pi r}=\frac{1}{2}jr\left(1.1\right).\]Электрическое поле ($\overrightarrow{E}$) параллельно оси провода. Вектор Умова - Пойнтинга ($\overrightarrow{P}$) направлен внутрь провода перпендикулярно его боковой поверхности. Получается, что электромагнитная энергия втекает внутрь провода извне. Если длина провода равна $l$, то количество электромагнитной энергии ($\triangle W$), которая за $1 с$ поступает в провод равна:
\[\triangle W=P\cdot 2\pi rl=EH\cdot 2\pi rl=E\frac{1}{2}jr\cdot 2\pi rl=\pi r^2lEj=VEj\left(1.2\right),\]где $V=\pi r^2l$ -- объем провода. В формуле (1.2) мы получили количество теплоты, которая выделяется при прохождении по проводнику электрического тока.
Ответ: Электромагнитная энергия поступает из окружающего пространства внутрь провода, затем выделяется как джоулево тепло.
Задание: Если $u$ - внутренняя энергия единицы объема среды, то $\delta A^{vnesh}=du$, или:
\[\frac{\partial u}{\partial t}=\overrightarrow{E}\dot{\overrightarrow{D}}+\overrightarrow{H}\dot{\overrightarrow{B}}+\overrightarrow{j}\overrightarrow{E}\left(2.1\right),\]покажите, что из уравнения (2.1) следует закон сохранения энергии для электромагнитного поля в дифференциальном виде.
Решение:
Для того чтобы преобразовать уравнение (2.1), используем уравнения Максвелла:
\[rot\overrightarrow{H}=\overrightarrow{j}+\frac{\partial \overrightarrow{D}}{\partial t}\ \left(2.2\right),\] \[rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\left(2.3\right).\]Правую часть уравнения (2.1) преобразуем к выражению:
\[\overrightarrow{E}\dot{\overrightarrow{D}}+\overrightarrow{H}\dot{\overrightarrow{B}}+\overrightarrow{j}\overrightarrow{E}=\overrightarrow{E}\left(\dot{\overrightarrow{D}}+\overrightarrow{j}\right)+\overrightarrow{H}\dot{\overrightarrow{B}}=\overrightarrow{E}rot\overrightarrow{H}-\overrightarrow{H}rot\overrightarrow{E}\ \left(2.4\right).\]Используем тождество:
\[div\left[\overrightarrow{E}\overrightarrow{H}\right]=-\overrightarrow{E}rot\overrightarrow{H}+\overrightarrow{H}rot\overrightarrow{E}\ \left(2.5\right).\]Тогда выражение (2.4) предстанет в виде:
\[\overrightarrow{E}\dot{\overrightarrow{D}}+\overrightarrow{H}\dot{\overrightarrow{B}}+\overrightarrow{j}\overrightarrow{E}=-div\left[\overrightarrow{E}\overrightarrow{H}\right]\left(2.6\right).\]Значит, выражение (2.1) получит вид:
\[\frac{\partial u}{\partial t}+div\left[\overrightarrow{E}\overrightarrow{H}\right]=0\ \left(2.7\right),\]где $\left[\overrightarrow{E}\overrightarrow{H}\right]=\overrightarrow{P}-\ $вектор Умова -- Пойнтинга.
Уравнение (2.7), есть закон сохранения энергии электромагнитного поля в дифференциальном виде.











