Закон Фарадея
Явление электромагнитной индукции было открыто Фарадеем экспериментально. Фарадей определил, что в замкнутом проводнике при изменении потока магнитной индукции возникает электрический ток. Правило, по которому определяют направление ЭДС индукции, сформулировал Ленц (индукционный ток направлен так, что создаваемое им поле препятствует изменению магнитного потока). Нейман дал математическое определение закона электромагнитной индукции в современной форме:
при этом контур считается неподвижным. Под $\frac{dФ}{dt}$ понимают полную скорость изменения потока индукции, охватываемого проводником в результате движения и деформации проводника и изменения магнитного поля. Закон Фарадея выражает новое физическое явление: изменяющееся магнитное поле порождает электрическое поле. Следовательно, электрическое поле порождается не только электрическими зарядами, но и изменяющимся магнитным полем.
Электрический ток может генерироваться движением магнитов, а проводники могут оставаться неподвижными.
Электромагнитная индукция является фундаментальным законом природы, который устанавливает связь между электрическими и магнитными полями.
Дифференциальная формулировка закона Фарадея
Используем определения ЭДС индукции вида:
потока:
где $L$ - контур, $S$ - поверхность, натянутая на контур $L$, $\overrightarrow{s}$ - вектор перемещения. Тогда закон Фарадея можно записать в виде:
Согласно формуле Стокса, имеем:
Подставим правую часть выражения (5) вместо левой части уравнения (4), получим:
где производная по времени - под знаком интеграла, так как площадь интегрирования не зависит от времени. Так как $S$ произвольна, то из (6) следует, что:
Уравнение (7) - дифференциальная форма записи закона электромагнитной индукции Фарадея. Это уравнение описывает закон возникновения электрического поля в точке за счет изменения магнитного поля в этой же точке. При этом поле $\overrightarrow{E}$ называют индукционным. Индукционное электрическое поле (в отличие от электростатического поля) не является потенциальным. В общем случае работа по перемещению заряда $q$ в индукционном электрическом поле по замкнутому контуру не равна нулю:
Задание: Вычислите полный заряд, который проходит по цепи, если в магнитном поле находится замкнутый проволочный контур, который в начальный момент времени пронизывает поток магнитной индукции, равный $Ф_1$. Поток уменьшается до нуля.
Решение:
Мгновенное значение ЭДС можно определить формулой:
\[{{\mathcal E}}_i=-\frac{dФ}{dt}\left(1.1\right).\]Согласно закону Ома, мгновенное значение силы тока ($I$) можно записать как:
\[I=-\frac{1}{R}\frac{dФ}{dt}\left(1.2\right),\]где $R$ - полное сопротивления цепи.
Заряд прошедший по цепи можно найти как:
\[q=\int{Idt\ \left(1.3\right).}\]Подставим в (1.3) выражение (1.2), получим:
\[q=-\frac{1}{R}\int\limits^0_{Ф_1}{dФ}=\frac{Ф}{R}.\]Данное выражение было получено Фарадеем. Он эмпирически заключил, что заряд, который проходит по цепи, пропорционален полному числу линий магнитной индукции, которые пересекает проводник, и обратно пропорционален сопротивлению цепи.
Ответ: $q=\frac{Ф}{R}.$
Задание: Найдите ЭДС индукции как функцию ${{\mathcal E}}_i$ от расстояния $x$ для квадратной рамки с током. Рамка имеет сторону $a$ и находится в одной плоскости с проводников с током силы $I$. Рамка движется поступательно с постоянной скоростью $v$. Направление движения указано на рис.1.
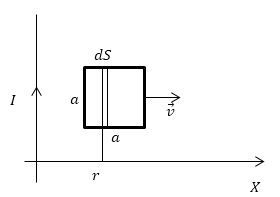
Рисунок 1.
Решение:
В качестве основания для решения задачи используем закон Фарадея:
\[{{\mathcal E}}_i=-\frac{dФ}{dt}\left(2.1\right).\]Для того чтобы получить искомую функцию ${{\mathcal E}}_i(x)$, построим функцию $Ф(x)$. Магнитное поле, в котором находится рамка, создается бесконечным проводником с током, оно может быть представлено как:
\[B=\frac{{\mu }_0I}{2\pi r}\left(2.2\right),\]где $r$ расстояние до точки, в которой рассматривается поле.
Выделим элемент площади $(dS)$ рамки, величина которого может быть выражена как:
\[dS=adr\left(2.3\right).\]В таком случае, элементарный магнитный поток через элемент квадратной рамки, используя выражения (2.2), (2.3) и определение потока, учитывая, что $\overrightarrow{B}\bot \overrightarrow{S}$, можно записать как:
\[dФ=BdS=\frac{{\mu }_0I}{2\pi r}adr\left(2.4\right).\]Вычислим полный поток, если $x\le r\le x+a$:
\[Ф=\int\limits^{x+a}_x{\frac{{\mu }_0I}{2\pi r}adr}=\frac{{\mu }_0Ia}{2\pi }ln\frac{x+a}{x}\left(2.5\right).\]Используя закон Фарадея (2.1) и выражение для магнитного потока (2.5) найдем ЭДС индукции:
\[{{\mathcal E}}_i=-\frac{dФ}{dx}\cdot \frac{dx}{dt}=-\frac{{\mu }_0Ia}{2\pi }\cdot \frac{x}{x+a}\left(x^{-1}-\left(x+a\right)x^{-2}\right)\cdot v=-\frac{{\mu }_0Ia}{2\pi }\cdot \frac{x}{x+a}\left(\frac{x-x-a}{x^2}\right)\cdot v=\frac{{\mu }_0Ia^2v}{2\pi \left(x+a\right)x}.\]Ответ: ${{\mathcal E}}_i$=$\frac{{\mu }_0Ia^2v}{2\pi \left(x+a\right)x}.$












