Характеристики ядра

Источник статьи

Автор24 — учеба по твоим правилам

Основными характеристиками атомных ядер, которые определяют их индивидуальность являются электрический заряд, масса, спин, энергия связи и т.д.

Заряд ядра

Ядро любого атома заряжено положительно. Носителем положительного заряда является протон. Поскольку заряд протона численно равен заряду электрона $e$, то можно записать что заряд ядра равен $+Ze$ ($Z$ -- целое число, которое указывает на порядковый номер химического элемента в периодической системе химических элементов Д. И. Менделеева). Число $Z$ также определяет количество протонов в ядре и количество электронов в атоме. Поэтому его называют атомным номером ядра. Электрический заряд является одной с основных характеристик атомного ядра, от которой зависят оптические, химические и другие свойства атомов.

Масса ядра

Другой важной характеристикой ядра является его масса. Массу атомов и ядер принято выражать в атомных единицах массы (а.е.м.). за атомную единицу массы принято считать $1/12$ массы нуклида углерода $^{12}_6C$:

где $N_A=6,022\cdot 10^{23}\ моль^-1$ -- число Авогадро.

Согласно соотношению Эйнштейна $E=mc^2$, массу атомов также выражают в единицах энергии. Поскольку:

масса протона $m_p=1.00728\ а.е.м.=938,28\ МэВ$,
масса нейтрона $m_n=1.00866\ а.е.м.=939,57\ МэВ$,
масса электрона $m_e=5,49\cdot 10^{-4}\ а.е.м.=0,511\ МэВ$,

Как видно масса электрона пренебрежительно мала в сравнении с массой ядра, то масса ядра почти совпадает с массой атома.

Масса отличается от целых чисел. Масса ядра, выражена в а.е.м. и округлена до целого числа называется массовым числом, обозначается буквой $A$ и определяет количество нуклонов в ядре. Число нейтронов в ядре равно $N=A-Z$.

Для обозначения ядер применяется символ $^A_ZX$, где под $X$ подразумевается химический символ данного элемента. Атомные ядра с одинаковым количеством протонов но разными массовыми числами называют изотопами. В некоторых элементов число стабильных и нестабильных изотопов достигает десятков, например, уран имеет $14$ изотопов: от $^{227}_{92}U\ $до $^{240}_{92}U$.

«Характеристики ядра» 👇

Помощь эксперта по теме работы

Найти эксперта

Решение задач от ИИ за 2 минуты

Решить задачу

Найди решение своей задачи среди 1 000 000 ответов

Найти

Большинство химических элементов существующих в природе, представляют собой смесь нескольких изотопов. Именно наличие изотопов объясняет тот факт, что некоторые природные элементы имеют массу, которая отличается от целых чисел. Например, природный хлор состоит с $75\%$ $^{35}_{17}Cl$ и $24\%$ $^{37}_{17}Cl$, а его атомная масса равна $35,5$ а.е.м. в большинства атомов, кроме водорода, изотопы имеют почти одинаковые физические и химические свойства. Но за своими исключительно ядерными свойствами изотопы существенно разнятся. Одни с них могут быть стабильными, другие -- радиоактивными.

Ядра с одинаковыми массовыми числами, но разными значениями $Z$ называют изобарами, например, $^{40}_{18}Ar$, $^{40}_{20}Ca$. Ядра с одинаковым количеством нейтронов называют изотонами. Среди легких ядер встречаются так называемые «зеркальные» пары ядер. Это такие пары ядер в которых числа $Z$ и $A-Z$ меняются местами. Примерами таких ядер могут быть $^{13}_6C\ $и $^{13_7}N$ или $^3_1H$ и $^3_2He$.

Размер атомного ядра

Считая атомное ядро приблизительно сферическим, можно ввести понятия его радиуса $R$. Отметим, что в некоторых ядрах есть небольшое отклонение от симметрии в распределении электрического заряда. Кроме того, атомные ядра не статические, а динамические системы, и понятие радиуса ядра не можно представлять как радиус шара. По этой причине, за размеры ядра необходимо брать ту область, в которой проявляются ядерные силы.

При создании количественной теории рассеивания $\alpha $ -- частиц Э. Резерфорд исходил с предположений, что атомное ядро и $\alpha $ -- частица взаимодействуют по закону Кулона, т.е. что электрическое поле вокруг ядра имеет сферическую симметрию. Рассеивание $\alpha $ -- частицы происходит в полном соответствии с формулой Резерфорда:

Это имеет место для $\alpha $ -- частиц энергия которых $E$ достаточно мала. При этом частица не способна преодолеть кулоновский потенциальный барьер и в последствии не достигает области действия ядерных сил. С увеличением энергии частицы до некоторого граничного значения $E_{гр}$ $\alpha $ -- частица достигает этой границы. Тога в рассеивании $\alpha $ -- частиц наблюдается отклонение от формулы Резерфорда. Из соотношения

Опыты показывают, что радиус $R$ ядра зависит от количества нуклонов, которые входят до состава ядра. Эта зависимость может выражаться эмпирической формулой:

где $R_0$ -- постоянная, $A$ -- массовое число.

Размеры ядер определяют экспериментально по рассеиванию протонов, быстрых нейтронов или электронов высоких энергий. Существует ряд других непрямых методов определения размеров ядер. Они обоснованы на связи время жизни $\alpha $ -- радиоактивных ядер с энергией выпущенных ими $\alpha $ -- частиц; на оптических свойствах, так называемых, мезоатомов, в которых один с электронов временно захвачен мюоном; на сравнении энергии связи пары зеркальных атомов. Эти методы подтверждают эмпирическую зависимость $R=R_0A^{1/3}$, а также с помощью этих измерений установлено значение постоянной $R_0=\left(1,2-1,5\right)\cdot 10^{-15}\ м$.

Отметим также, что за единицу расстояний в атомной физике и физике элементарных частиц берут единицу измерения «ферми», который равняется ${10}^{-15}\ м$ (1 ф=${10}^{-15}\ м)$.

Радиусы атомных ядер зависят от их массового числа и находятся в промежутке от $2\cdot 10^{-15}\ м\ до\ 10^{-14}\ м$. если с формулы $R=R_0A^{1/3}$ выразить $R_0$ и записать его в виде $\left(\frac{4\pi R^3}{3A}\right)=const$, то можно увидеть что на каждый нуклон припадает приблизительно одинаковый объем. Это значит, что плотность ядерного вещества для всех ядер так же приблизительно одинакова. Выходя с существующих ведомостей о размерах атомных ядер, найдем среднее значение плотности вещества ядра:

Как видим, плотность ядерного вещества очень большая. Это обусловлено действием ядерных сил.

Энергия связи. Дефект масс ядер

При сравнении суммы масс покоя нуклонов, которые образуют ядро с массой ядра было замечено, что для всех химических элементов справедливо неравенство:

где $m_p$ -- масса протона, $m_n$ -- масса нейтрона, $m_я$ -- масса ядра. Величину $\triangle m$, что выражает разницу масс между массой нуклонов, которые образуют ядро, и массой ядра, называют дефектом массы ядра

Важные сведения о свойствах ядра можно получить не вникая в подробности взаимодействия между нуклонами ядра, на основании закона сохранения энергии и закона пропорциональности массы и энергии. По сколько в результате любого изменения массы $\triangle m$ происходит соответствующее изменение энергии $\triangle E$ ($\triangle E=\triangle mc^2$), то при образовании ядра выделяется определенное количество энергии. По закону сохранения энергии такое же количество энергии необходимо, чтоб разделить ядро на составляющие частицы, т.е. отдалить нуклоны один от одного на такие же расстояния, при которых отсутствует взаимодействие между ними. Эту энергию называют энергией связи ядра.

Если ядро имеет $Z$ протонов и массовое число $A$, то энергия связи равна:

Замечание 1

Отметим, что этой формулой не совсем удобно пользоваться, т.к. в таблицах приводиться не массы ядер, а массы, которые определяют массы нейтральных атомов. Поэтому для удобства вычислений формулу преобразуют таким образом, чтобы в нее входили массы атомов, а не ядер. С этой целью в правой части формулы добавим и отнимем массу $Z$ электронов $(m_e)$. Тогда

\[E_{св}=\left[Z\left(m_p+m_e\right)+\left(A-Z\right)m_n-(m_я+Zm_e)\right]c^2==\left[Zm_{{}^1_1H}+\left(A-Z\right)m_n-m_a\right]c^2.\]

$m_{{}^1_1H}$ -- масса атома водорода, $m_a$ -- масса атома.

В ядерной физике энергию часто выражают в мегаэлектрон-вольтах (МэВ). Если речь идет о практическом применении ядерной энергии, то ее измеряют в джоулях. В случае сравнения энергии двух ядер используют массовую единицу энергии -- соотношение между массой и энергией ($E=mc^2$). Массовая единица энергии ($le$) равняется энергии, что соответствует массе в одну а.е.м. Она равняется $931,502$ МэВ.

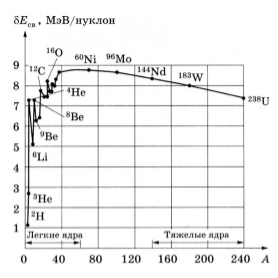
Рисунок 1.

Кроме энергии, важное значение имеет удельная энергия связи -- энергия связи, которая припадает на один нуклон: $w=E_{св}/A$. Эта величина меняется сравнительно медленно по сравнению со сменой массового числа $A$, имея почти постоянную величину $8.6$ МэВ в средней части периодической системы и уменьшается до ее краев.

Для примера рассчитаем дефект массы, энергию связи и удельную энергию связи ядра атома гелия.