Напомню, что испускательной способность абсолютно черного тела определяется универсальной функцией Кирхгофа. При теоретических исследованиях для характеристики спектрального состава равновесного излучения удобнее использовать ее как функцию частоты: ${\varepsilon }_{\nu ,T\ }={\varepsilon }_{\nu ,T\ }(\nu ,T)$. В экспериментальных работах чаще ее представляют, как функцию длины волны: ${\varepsilon }_{\lambda ,T\ }={\varepsilon }_{\lambda ,T\ }(\lambda ,T)$. Связь между этими функциями реализуется следующим образом. Так, если по известной функции ${\varepsilon }_{\nu ,T\ }(\nu ,T)$ необходимо найти ${\varepsilon }_{\lambda ,T\ }$, надо провести следующую последовательность действий: в функции ${\varepsilon }_{\nu ,T\ }$частота $\nu $ заменяется на $\frac{2\pi c}{\lambda }$ и получившееся выражение умножается на $\frac{2\pi c}{{\lambda }^2}$, то есть:
В 1893 г. Вин показал, что функция спектрального распределения должна иметь следующий вид:
где $F\left(\frac{\nu }{T}\right)$- неизвестная функция отношения частоты к термодинамической температуре. Для ${\varepsilon }_{\lambda ,T\ }$ согласно формуле (1) получается уравнение:
где $\varphi \left(\lambda T\right)$ -- неизвестная функция от произведения длины волны на температуру. Найдем длину волны (${\lambda }_m$), которой соответствует максимум функции ${\varepsilon }_{\lambda ,T\ }$. Для этого продифференцируем уравнение (3) по длине волны, получим:
Выражение $\lambda T{\varphi }'\left(\lambda T\right)-5\varphi \left(\lambda T\right)$ есть некоторая функция $\sigma (\lambda T)$. Понятно, что при $\lambda ={\lambda }_m$ $\frac{d{\varepsilon }_{\lambda ,T\ }}{d\lambda }=0$. Следовательно, запишем, что:
Так как длинна волны не может быть бесконечно большой, следовательно, равна нуль при $\lambda ={\lambda }_m$ функция $\sigma \left({\lambda }_mT\right)=0.$ Решение последнего уравнения относительно произведения ${\lambda }_mT\ $ дает некоторое постоянное число, которое обозначим буквой b. Так, получаем равенство:
Уравнение (8) носит название закона смещения Вина.
Значение постоянной b, полученное в эксперименте равно: $b=2.9\cdot {10}^{-3}м\cdot K$.
Закон смещения объясняет, причину преобладания в спектре тел длинных волн при понижении их температуры.
И так увеличением температуры абсолютно черного тела максимум плотности излучения в его спектре смещается на более короткие длины волн (или на большие частоты) (рис.1).
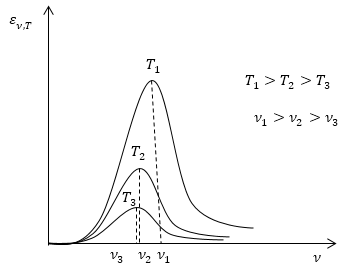
Рис. 1
Площадь, которая ограничена кривой функции ${\varepsilon }_{\nu ,T~}(\nu )$ и осью абсцисс, пропорциональна температуре в четвертой степени.
Задание: Максимум спектральной плотности энергетической светимости звезды приходится на длину волны ${\lambda }_m=580\ нм.$ Считая, что звезда излучает как абсолютно черное тело, определить температуру поверхности звезды.
Решение:
В качестве основы для решения задачи используем закон смещения Вина:
\[{\lambda }_mT=b\ \left(1.1\right).\]Выразим из него искомую температуру, получим:
\[T=\frac{b}{{\lambda }_m}\ \left(1.2\right).\]Переведем длину волны в СИ, получим: ${\lambda }_m=580\ нм=580\cdot {10}^{-9}м.$ Помним, что постоянная Вина $b=2.9\cdot {10}^{-3}м\cdot K.$ Подставим численные значения величин, проведем расчет:
\[T=\frac{2.9\cdot {10}^{-3}}{580\cdot {10}^{-9}}=5\cdot {10}^3\ \left(К\right).\]Ответ: Температура поверхности этой звезды равна 5 кК.
Задание: Энергетическая светимость абсолютно черного тела равна${\varepsilon }_T=3\cdot {10}^4\frac{Вт}{м^2}$. Какова длина волны максимума испускательной способности данного тела?
Решение:
В качестве основы для решения задачи используем закон Стефана -- Больцмана и закон смещения Вина.
Первый из них:
\[{\varepsilon }_T= \sigma T^4\left(2.1\right),\]где $\sigma=5,67{\cdot 10}^{-8}(Вт\cdot м^{-2}\cdot К^{-4})$- постоянная Стефана -- Больцмана.
Второй из используемых законов:
\[{\lambda }_mT=b\ \left(2.2\right).\]Выразим температуру тела из (2.1), получим:
\[T=\sqrt[4]{\frac{{\varepsilon }_T}{\sigma}}\ \left(2.3\right).\]Из (2.2) выразим длину волны, получим:
\[{\lambda }_m=\frac{b}{T}\ \left(2.4\right).\]Подставляя в (2.4), температуру, полученную в (2.3), получим выражение искомой длины волны:
\[{\lambda }_m=b\sqrt[4]{\frac{\sigma}{{\varepsilon }_T}}\]Постоянная Вина равна $b=2.9\cdot {10}^{-3}м\cdot K.$ Подставим численные значения величин, проведем расчет:
\[{\lambda }_m=2.9\cdot {10}^{-3}\sqrt[4]{\frac{5,67{\cdot 10}^{-8}}{3\cdot {10}^4}}=3,4{\cdot 10}^{-6}(м)\]Ответ: Длина волны 3,4 мкм.











