Как говорилось в разделе, посвященном тепловому двигателю, эффективность тепловой машины характеризуют с помощью коэффициента полезного действия (КПД), который определен как:
или:
где $Q_n$ - количество теплоты, переданное рабочему телу от нагревателя, ${Q'}_{ch}$ - количество теплоты, переданное газом холодильнику. Возможность создания такой тепловой машины, КПД которой равен 1, не противоречит первому началу термодинамики. Такая машина могла бы превращать все количество теплоты, которое получает от нагревателя в работу. По своему значению она не уступала бы вечному двигателю первого рода, так как с ее помощью можно было бы производить работу за счет неисчерпаемой внутренней энергии, например, мирового океана. Такую машину Вильгельм Освальд назвал вечным двигателем второго рода. Но уже Сади Карно понял, что такая машина принципиально невозможна. Опытные факты говорят о том, что построение вечного двигателя второго рода невозможно и это возведено в постулат. Это и называют вторым началом термодинамики. Второе начало термодинамики - результат обобщения опытных фактов. Существует несколько формулировок второго начала термодинамики.
Формулировка Вильяма Томсона
Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара. Под тепловым резервуаром понимают систему тел в состоянии термодинамического равновесия, обладающую запасом внутренней энергии. Сам резервуар работы не совершает, а только передает теплоту. На первый взгляд может показаться, что, например, изотермический процесс противоречит данной формулировке. При $T=const$ в соответствии с первым началом термодинамики, все тепло преданное системе идет на выполнение данной системой работы. Однако в формулировке существенно указание на то, что процесс круговой.
Формулировка Планка
Нельзя создать построить периодически действующую машину, единственным результатом которой было бы поднятие груза за счет охлаждения теплового резервуара. Опять таки мы видим указание на периодичность, которое крайне важно. Формулировка Планка лишь по форме отличается от формулировки Томсона.
Клаузиус дал принципиально иную формулировку. Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому. Под теплотой здесь следует понимать внутреннюю энергию. Имеется в виду не только передача тепла при тепловом контакте, но и передача любого рода. Постулат Клаузиуса не утверждает, что невозможно передать тепло от тела с меньшей температурой к более нагретому в принципе. Это невозможно при условии, что во всех остальных телах никаких изменений не происходит.
И еще одна формулировка второго начала термодинамики касается энтропии. Допустим, что система замкнута и изолирована. Она переходит из состояния (1) в состояние (2) (рис 1) путь $L_1$. Процесс возвращения системы из 2 в 1 существует и он обратим путь $L_2$.
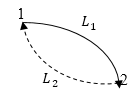
Рис. 1
Как видно из рисунка (рис.1) образовался цикл, к которому можно применить неравенство Клаузиуса (см. соответствующий раздел):
Как было сказано, что в процессе 1-2 система была изолированной, следовательно, $\delta Q\ $в интегралу по пути $L_1$ равен нулю:
В обратимом переходе 2-1 можно записать:
Следовательно, неравенство (3) запишем:
Или
Неравенство (7) означает, что при переходе замкнутой системы из состояния с энтропией $S_1$ в состояние с энтропией $S_2$ энтропия или увеличивается, или остается постоянной. Выражение (7) и есть очередная формулировка второго начала термодинамики. В процессах, происходящих в изолированных системах, энтропия не убывает. В неизолированных системах энтропия может и убывать и возрастать, и не изменяться. Важно, что энтропия в замкнутых системах не изменяется только в обратимых процессах. В необратимых процессах она растет. Рост энтропии означает приближение системы к состоянию термодинамического равновесия.
Таким образом, первое начало термодинамики говорит о количественных отношениях между величинами, которые характеризуют систему при различных изменениях, но не говорит о направлении этих изменений. Второе начало термодинамики указывает на направление, в которых эти изменения должны произойти.
Задание: Найдите КПД цикла, который представлен на рисунке 2 (рис.2). Отношение максимального давления к минимальному в цикле составляет n. Рабочее тело -- идеальный газ с показателем адиабаты $𝛾$.
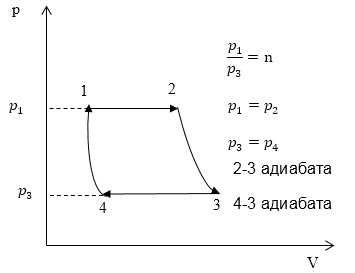
Рис. 2
Решение:
Основой для решения станет определение КПД в виде:
\[\eta =\frac{Q_n-{Q'}_{ch}}{Q_n}\left(1.1\right),\]где $Q_n$- количество теплоты, переданное рабочему телу от нагревателя, ${Q'}_{ch}$ - количество теплоты, переданное газом холодильнику.
Определим процессы, в которых тепло газу подводится:
Адиабатные процессы идут без подвода и отвода тела, температура газа растет в процессе 1-2, делаем вывод о том, что тепло подводят в процессе 1-2. Найдем количество теплоты, подведенное в этом процессе газу:
\[\triangle Q_{12}=\frac{i}{2}\nu R\left(T_2-T_1\right)+p_1\left(V_2-V_1\right)=\frac{i}{2}\nu R\left(T_2-T_1\right)+\nu R\left(T_2-T_1\right)=\frac{i}{2}\nu R\left(T_2-T_1\right)\left(\frac{i}{2}+1\right)\left(1.2\right),\]при преобразовании уравнения (1.2) используется уравнение Менделеева -- Клайперона, которое записывается для состояния 1 и 2, а именно:
\[p_1V_1=\nu RT_1,p_2V_2=\nu RT_2\to p_1V_2=\nu RT_2\left(1.3\right),\]причем надо учесть, что $p_1=p_2$ по условию задачи (рис.2). Имеем в виду, что $Q_n=\triangle Q_{12}$.
Найдем количество тепла, отданное холодильнику (${Q'}_{ch}$). Тепло газом отдается в процессе 3-4. Найдем количество этого тепла, причем имеем в виду, что ${Q'}_{ch}=-\triangle Q_{34}$:
\[\triangle Q_{34}=\frac{i}{2}нR\left(T_4-T_3\right)+p_3\left(V_4-V_3\right)=\frac{i}{2}нR\left(T_4-T_3\right)+нR\left(T_4-T_3\right)=нR\left(T_4-T_3\right)\left(\frac{i}{2}+1\right)\left(1.4\right).\]Преобразования уравнения (1.4) аналогичны уравнению (1.3).
Для того чтобы определить как соотносятся разности температур в уравнениях (1.3) и (1.4) запишем уравнения адиабаты для состояний (2) (3), а затем состояний (4) и (1) в параметрах $p,T$ получим:
\[T^{\gamma }_2p^{1-\gamma }_1=T^{\gamma }_3p^{1-\gamma }_3\to T_2p^{\frac{1-\gamma }{\gamma }}_1=T_3p^{\frac{1-\gamma }{\gamma }}_3\ \left(введем\ обозначение\ a=\frac{1-\gamma }{\gamma }\right)\to T_3=T_2{\left(\frac{p_1}{p_3}\right)}^a\to T_3=T_2n^a\left(1.5\right).\]Для состояний (4) и (1) аналогично получаем:
\[T_4=T_1n^a\ \left(1.6\right).\]Найдем $\left(T_4-T_3\right),$ используем (1.5) и (1.6), получаем:
\[\left(T_4-T_3\right)=n^a\left(T_1-T_2\right)\left(1.7\right).\]Найдем КПД, используя формулу (1.1), получаем:
\[\eta =\frac{\triangle Q_{12}+\triangle Q_{34}}{\triangle Q_{12}}=\frac{\frac{i}{2}\nu R\left(T_2-T_1\right)\left(\frac{i}{2}+1\right)+\nu R\left(T_4-T_3\right)\left(\frac{i}{2}+1\right)}{\frac{i}{2}\nu R\left(T_2-T_1\right)\left(\frac{i}{2}+1\right)}=\frac{\frac{i}{2}\nu R\left(T_2-T_1\right)\left(\frac{i}{2}+1\right)+\nu Rn^a\left(T_1-T_2\right)\left(\frac{i}{2}+1\right)}{\frac{i}{2}\nu R\left(T_2-T_1\right)\left(\frac{i}{2}+1\right)}=1-n^a=1-n^{\frac{1-\gamma }{\gamma }}\ \left(1.8\right).\]Ответ: КПД в цикле (рис.2) $\eta =1-n^{\frac{1-\gamma }{\gamma }}$.
Задание: Эффективным способом увеличения КПД является повышение температуры нагревателя тепловой машины. Делают паровые котлы высокого давления, в которых температура пара достигает до 5000С и температура холодильника 00С. Каково КПД такой машины?
Решение:
Если считать тепловую машину идеальной (см. раздел Тепловой двигатель), то КПД можно вычислить как:
\[\eta =\frac{T_n-T_{ch}}{T_n}\ \left(2.1\right),\]где $T_n$- температура нагревателя, $T_{ch}$ -температура холодильника.
Переведем заданные температуры в СИ:
\[T_n=500+273=773\ \left(К\right).\] \[T_{ch}=0+273=273\left(К\right).\]Проведем вычисления:
\[\eta =\frac{773-273}{273}=0,65=65\%\]Ответ: КПД данного парового котла 65%.











