Закон сохранения энергии для количества теплоты как формы энергии может быть записан в виде:
\[\delta Q=dU+\delta A\ \left(1\right).\]или
\[CdT=dU+\delta A\ \left(2\right),\]где C -- теплоемкость системы.
В термодинамике уравнение (1) является крайне важным и называется первым началом. В отличие от закона сохранения их механики, первое начало термодинамики содержит бесконечно малое количество теплоты $\delta Q$. Мы знаем, что изучение разного рода переходов именно этой формы энергии -- предмет термодинамики. Очень часто уравнение (1) записывается в виде:
\[\delta Q=dU+pdV\ \left(3\right).\]Уравнения (1), (2) и (3) записаны в дифференциальной форме.
В связи с тем, что теплота и работа не являются функциями состояния, то для бесконечно малого количества теплоты и элементарной работы используют обозначение $\delta Q$, а не $dQ$ и $\delta A$, а не $dA$. Этим подчёркивается, что $\delta Q$ и $\delta A$ не рассматриваются как полные дифференциалы, т.е. невсегда могут быть представлены как бесконечно малые приращения функций состояния (только в частных случаях).
Первое начало термодинамики не может предсказать направление развития процесса. Этот закон лишь констатирует факт изменения величин в процессе и говорит о величине их изменения. Забегая вперед, скажем, что второе начало термодинамики определяет направление процесса.
В том случае, если рассматривается круговой процесс (система возвращается в исходное состояние), изменение внутренней энергии системы $dU=0$, то первое начало термодинамики говорит о том, что все тепло, которое получила система, идет на совершение этой системой работы.
Интегральная форма первого начала термодинамики
Первое начало термодинамики можно записать и в интегральной форме:
\[Q=\triangle U+A\ \left(4\right).\]На словах уравнение (4) означает, что подводимая к системе теплота идет на изменение внутренней энергии системы и совершение этой системой работы.
Обратимся опять к круговому процессу ($\triangle U$). Если в круговом процессе $Q=0,\ то\ A=0.$ Это означает, что невозможен процесс производства работы без какого-то ни было изменения во внешних к системе телах. Или говорят по-другому: не возможен вечный двигатель первого рода.
Рассмотрим изохорный процесс. При постоянном объеме система работу не совершает. В таком случае:
\[Q=\triangle U\left(5\right)\]говорят, что все подводимое к системе тепло идет на изменение (увеличение) внутренней энергии системы.
В изотермическом процессе внутренняя энергия системы неизменна, следовательно:
\[Q=A\ \left(6\right)\]все подводимое системе тепло идет на совершение системой работы.
Задание: В идеальном газе совершается процесс заданный уравнением: $T=T_0e^{aV}$, где $T_0,\ a-\ $ постоянные. Изохорная молярная теплоемкость газа $c_{\mu V}$ известна. Найти $c_{\mu }$(V) для заданного процесса.
Решение:
Основой для решения будет первое начало термодинамики в дифференциальном виде:
\[CdT=dU+\delta A\ \left(1.1\right).\]Приращение внутренней энергии $dU$ равно:
\[dU=\frac{i}{2}\nu RdT\ \to CdT=\frac{i}{2}\nu RdT\ +pdV\left(1.2\right),\]где $\delta A=pdV$.
Используем для дальнейших вычислений уравнение Менделеева -- Клайперона:
\[pV=\nu RT\left(1.3\right).\]Подставим в (1.3) вместо T уравнение процесса, получим:
\[pV=\nu RT_0e^{aV}\to p=\nu RT_0\frac{e^{aV}}{V}\ \left(1.4\right).\]Так как из уравнения процесса $dT$ равно:
\[dT=aT_0e^{aV}dV(1.5),\]То, подставив (1.5) и (1.4) в (1.2), получим выражение:
\[C{\cdot a\cdot T}_0e^{aV}dV=\frac{i}{2}a\cdot \nu RT_0e^{aV}dV\ +\nu RT_0\frac{e^{aV}}{V}dV\to C=\frac{i}{2}\nu R\ +\frac{\nu R}{a\cdot V}\left(1.6\right).\]Соответственно, для молярной теплоемкости процесса получим:
\[c_{\mu }\left(V\right)=\frac{C}{\nu }=\frac{i}{2}R\ +\frac{R}{aV}=c_{\mu V}+\frac{R}{aV}\ \left(1.7\right).\]Ответ: Молярная теплоемкость для заданного процесса выражается формулой: $c_{\mu }\left(V\right)=c_{мV}+\frac{R}{aV}$.
Задание: На рис.1 представлен процесс, состоящий из изотермы (1) и адиабаты (2). Укажите площадь, которая представляет количество теплоты, которое поглощает газ.
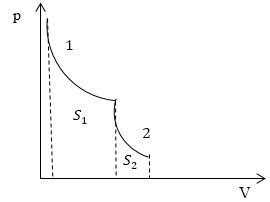
Рис. 1
Запишем первое начало термодинамики в интегральном виде:
\[Q=\triangle U+A\ \left(2.1\right).\]Первая часть процесса, который представлен на рис.1, является изотермой, следовательно: $\triangle U_1=0$ и уравнение (2.1) запишется, как:
\[Q_1=A_1\ \left(2.2\right).\]Вторая часть процесса представлена адиабатой. Относительно адиабатных процессов известно, что они проводятся без подвода тепла, следовательно:
\[Q_2=0\ \left(2.3\right),\]а работа по расширению газа идет за счет уменьшения его внутренней энергии.
Итак, мы получили, что в указанном на рис.1 процессе тепло подводится только на участке 1, и оно равно работе, которую совершает газ в процессе своего расширения. По определению в процессе 1 работа равна:
\[A_1=\int\limits^{V_2}_{V_1}{pdV\ \left(2.4\right).}\]Из геометрического свойства интеграла $A_1=S_1$ на рис. 1.
Следовательно, получается:
\[Q_1=A_1=S_1.\]Ответ: Количество теплоты, подведенное в заданном процессе, представлено площадью $S_1$ на рис. 1.












