Что такое фаза
Фазой называют однородную с физической точки зрения, макроскопическую часть вещества, которая отделена границами раздела от других частей системы, таким образом, что ее можно извлечь из системы механическим способом.
Например, система жидкость -- пар является двухфазной. Не может быть более одной газообразной фазы, так как газы смешиваются.
Важным вопросом при наличии несколько фаз является вопрос об условиях, при которых система находится в равновесии. Равновесие будет включать как механическое, так и тепловое равновесие. Для того, чтобы система находилась в тепловом равновесии необходимо, чтобы температура во всех ее точках была одинакова. Для механического равновесия необходимо, чтобы давления по разные стороны границы раздела соприкасающихся фаз были одинаковы. Это условие строго справедливо только для плоских границ. В случае кривых границ оно нарушается действие сил поверхностного натяжения. Влияние этой кривизны учтем позднее. Как уже сказано, равенство давлений и температур -- необходимое, но не достаточное условие равновесия, так как соприкасающиеся фазы могут переходить друг в друга. Это так называемые фазовые переходы. При таких переходах одни фазы растут, другие уменьшаются вплоть до исчезновения. Состояние равновесия должно характеризоваться тем, что массы всех фаз, составляющих систему, не изменяются. Таким образом, в системе, в которую входит несколько фаз возникает еще одно условие равновесия: равновесие взаимных превращений фаз. Изменение агрегатного состояния вещества - фазовое превращение.
Состояние динамического равновесия
Когда число молекул, которые переходят из жидкости в пар, такое же, как количество молекул, переходящих из пара в жидкость, мы говорим о состояние динамического или статистического равновесия, в этом состоянии количество вещества в каждой фазе в среднем остается неизменным. Фазовое равновесие между любыми фазами 1 и 2 не является статическим состоянием, в котором полностью прекратились фазовые превращения. Оно характеризуется равенством средних скоростей двух взаимно противоположных процессов: превращением фазы 1 в фазу 2 и обратно. При равновесии эти противоположные процессы взаимно компенсируют друг друга, то есть выполняется принцип детального равновесия. При этом количество вещества в каждой фазе в среднем остается неизменным.
Рассмотрим систему, которая состоит из двух фаз (1 и 2), которые могут переходить друг в друга. Пусть $m_1\ $масса первой фазы, $m_2$ масса второй фазы. Удельные термодинамические потенциалы вещества этих фаз обозначим ${\varphi }_1$ и ${\varphi }_2$. Термодинамический потенциал (энергия Гиббса) всей системы будет, в этом случае иметь вид:
\[Ф=m_1{\varphi }_1+m_2{\varphi }_2\left(1\right).\]Пусть давление и температура в системе поддерживаются постоянными. В таком случае ${\varphi }_1$ и ${\varphi }_2$ не будут изменяться потому, что эти потенциалы, являются функциями температуры и давления. Полная масса системы $m_1+m_2=m=const.$ Изменяются массы отдельных фаз, при этом изменения должны происходить в таком направлении, при котором энергия Гиббса $\ (Ф=U+pV-TS$) приняла бы минимальное значение. Если ${\varphi }_1$ $>$ ${\varphi }_2$, то любое превращение фазы 1 в фазу 2 сопровождается уменьшением Ф. Этот переход будет происходить до тех пор, пока вещество из фазы 1 полностью не перейдет в фазу 2. Система станет однофазной. Тогда термодинамический потенциал системы примет минимальное значение равное $m{\varphi }_2$. Если мы имеем обратную ситуацию (${\varphi }_1$ $ \[{\varphi }_1\left(p,T\right)={\varphi }_2\left(p,T\right)(2)\]
фазы будут находиться в равновесии друг с другом. Можно сделать вывод о том, что условием равновесия фаз является равенство их удельных термодинамических потенциалов.
Мы знаем, что внутренняя энергия системы (U) и энтропия (S) определены с точностью до постоянных. Следовательно, энергия Гиббса (Ф) и его удельное значение $\varphi \left(p,T\right)$ определены с точностью до произвольной линейной функции температуры. Возникающую в (2) неоднозначность следует исключить. Для этого договариваются определять $\varphi \left(p,T\right)$ интегрируя выражение:
\[d\varphi =-sdT+vdp\ (3)\]исходя из одного и того же начального состояния. В выражении (3) $v\ $- удельный объем.
Смысл условия равновесия (2): При любых фазовых переходах величина удельного термодинамического потенциала неизменна. В данных условиях удельный термодинамический потенциал всегда изменяется непрерывно. Это отличие удельного термодинамического потенциала от других физических параметров, например, удельного объема, удельной энтропии и прочих, которые изменяются скачкообразно.
Задание: Рассмотреть газ Ван-дер-Ваальса. Докажите правило Максвелла относительно площадей для изотермы Ван-дер-Ваальса. Укажите, где находятся точки фазового превращения, используя условие равновесия.
Решение:
Применим к процессу превращения жидкости в пар и обратно условие равновесия:
\[{\varphi }_1\left(p,T\right)={\varphi }_2\left(p,T\right)\left(1.1\right).\]Рассмотрим изотерму вещества при температуре ниже критической (рис. 1):
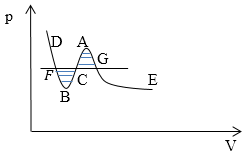
Рис. 1
На рис. 1 ветви GE и FD -- соответствуют устойчивым состояниям вещества (газообразному и жидкому). Участок GA соответствует пересыщенному пару, участок FB -- перегретой жидкости. Участок BCA -- отображает абсолютно не устойчивое состояние вещества. Горизонтальный участок FCG -- представляет изотерму вещества в двухфазном состоянии.
Когда точка перемещается вдоль изотермы, имеется в виду, что dT=0 (температура постоянна), в таком случае можно из выражения для удельного термодинамического потенциала:
\[d\varphi =-sdT+vdp\left(1.2\right)\]можно записать:
\[d\varphi =vdp\to \varphi =\int{vdp}\left(1.3\right).\]Так как интегрирование у нас в уравнении (1.4) идет по переменной p, нам удобнее перевернуть оси (рис.2).
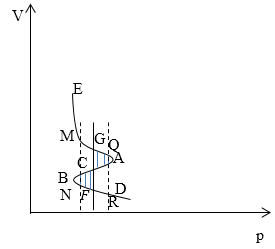
Рис. 2
Рассмотрим изменение функции $\varphi \left(p,T\right)\ $при перемещении точки вдоль изотермы EACBD (рис. 2). На участке EA dp положительный, следовательно $\varphi \left(p,T\right)$ возрастает. На участке ACD dp меняет знак, а потом убывает, $\varphi \left(p,T\right)$ начинает убывать. Далее если двигаться по изотерме, на участке BD потенциал $\varphi \left(p,T\right)$ снова начинает возрастать. Величина $\varphi \left(p,T\right)$ будет проходить через те же значения, которые она на ветви AE. Следовательно, существует изобара GF, в точках которой значения $\varphi \left(p,T\right)$ одинаковы:
\[{\varphi }_G\left(p,T\right)={\varphi }_L\left(p,T\right)\ \left(1.4\right).\]Из (1.4), следует, что:
\[\int\nolimits_{GACBF}{vdp}=0\to \int\nolimits_{GAC}{vdp=\int\nolimits_{FBC}{vdp}}\ \left(1.5\right).\]Это значит, что заштрихованные площади GACD и CBFC на рис. 1 и рис.2 одинаковы. Проведем две изобары MN и QR справа и слева от изобары GF. Тогда можно записать следующее:
\[{\varphi }_M={\varphi }_G-\int\limits^{p_G}_{p_M}{v_pdp,}\ {\varphi }_N={\varphi }_F-\int\limits^{p_F}_{p_N}{v_gdp,}\]где $v_p$- удельный объем пара, $v_g$- удельный объем жидкости. Так как ${\varphi }_G=ц_F,$ $v_p>v_g$, пределы интегрирования одни и те же, то ${\varphi }_M
Задание: В теплоизолированном сосуде система состоит изо льда и насыщенного водяного пара. Насколько необходимо повысить давление воздуха в сосуде, чтобы давление пара надо льдом повысилось на один процент, если температура постоянна (T), удельный объем льда равен $v_i$?
Решение:
Изменение термодинамического потенциала при изменении давления $\triangle p$ приводит к изменению удельного термодинамического потенциала на ($\triangle {\varphi }_i$):
\[\triangle {\varphi }_i=v_i\triangle p\ \left(2.1\right).\]Для сохранения равновесия изменение термодинамического потенциала пара должно быть таким же, но для пара мы можем записать ($\triangle {\varphi }_p$):
\[\triangle {\varphi }_p=v_p\triangle p_p=\frac{RT}{\mu }\frac{\triangle p_p}{p_p}\left(2.2\right).\]Приравняем (2.1) и (2.2), получим:
\[\triangle {\varphi }_i=\triangle {\varphi }_p;v_i\triangle p=\frac{RT}{м}\frac{\triangle p_p}{p_p}\to \triangle p=\frac{RT}{\mu v_i}\frac{\triangle p_p}{p_p}=0,01\cdot \frac{RT}{\mu v_i}\]Ответ: Давление воздуха в сосуде надо повысить на $\triangle p=0,01\cdot \frac{RT}{\mu v_i}$.











