Что такое энтропия
Энтропией называют функцию состояния системы (S), дифференциал которой в бесконечно малом обратимом процессе равен:
\[dS=\frac{\delta Q}{T}\left(1\right),\]где $\delta Q$- элементарное тепло, сообщенное системе, T -- температура системы.
По знаку изменения энтропии системы в обратимом процессе можно судить о направлении обмена теплом. С помощью формулы (1) можно найти только изменение энтропии. Отметим, что выражение (1) справедливо только для обратимых процессов.
Определим физический смысл энтропии, обратившись к модели идеального газа. Возьмем один моль газа. Запишем первое начало термодинамики в дифференциальной форме:
\[\delta Q=dU+pdV\ \left(2\right).\]Разделим правую и левую части выражения (2) на температуру T, получим:
\[\frac{\delta Q}{T}=\frac{dU}{T}+\frac{pdV}{T}=с_{\mu V}\frac{dT}{T}+\frac{pdV}{T}\ \left(3\right),\]где $с_{\mu V}=\frac{i}{2}R$. Используем уравнение Менделеева -- Клайперона, выразим из него $\frac{p}{T}$:
\[pV=RT\to \frac{p}{T}=\frac{R}{V}\left(4\right).\]Подставим (4) в (3), получаем:
\[\frac{\delta Q}{T}=с_{мV}\frac{dT}{T}+\frac{RdV}{V}=d\left(с_{мV}lnT+RlnV\right)\left(5\right).\]В правой части выражения (5) мы получили полный дифференциал, следовательно, слева должен быть так же полный дифференциал. В выражении (1) это дифференциал назван $dS$.
Применим формулу (5) для вычисления $\triangle S$ в изотермическом процессе. При T=const внутренняя энергия системы не изменяется. Получаем, что
\[dS=RdlnV\to \int\limits^{(2)}_{(1)}{dS=R\int\limits^{(2)}_{(1)}{dlnV=S_2-S_1=Rln\frac{V_2}{V_1}}}\ \left(6\right).\]Используем связь объема, который занимает газ в состоянии равновесия с числом пространственных микросостояний частиц газа, которая дается формулой:
\[Г_0=\frac{N!}{\left(N-n\right)!}\left(7\right),\]где $Г_0$- полное число микросостояний системы, $N$ - число ячеек, в которые можно поместить частицы системы, $n$ - количество частиц. Мы рассматриваем 1 моль газа, следовательно, $n = N_A.$ Поэтому формула (7) для объемов $V_1\ $и $V_2$ из (6) имеет вид:
\[Г_{01}=\frac{N_1!}{\left(N_1-N_A\right)!},\ Г_{02}=\frac{N_2!}{\left(N_2-N_A\right)!}\left(8\right),\]где $N_1=\frac{V_1}{l^3}$, $N_2=\frac{V_2}{l^3},\ l={10}^{-10}м.$ Используем формулу Стирлинга (при больших $n\ n!\approx {\left(\frac{n}{e}\right)}^n$), получаем:
\[\frac{Г_{02}}{Г_{01}}\approx {\left(\frac{N_2}{N_1}\right)}^{N_A}={\left(\frac{V_2}{V_1}\right)}^{N_A}\left(9\right).\]Найдем логарифм от выражения (9), получим:
\[ln\frac{V_2}{V_1}=\frac{1}{N_A}ln\frac{Г_{02}}{Г_{01}}\ \left(10\right).\]Следовательно,
\[S_2-S_1=Rln\frac{V_2}{V_1}=\frac{R}{N_A}ln\frac{Г_{02}}{Г_{01}}=klnГ_{02}-klnГ_{01}\left(11\right),\]где $k$ - постоянная Больцмана.
Формула Больцмана
Вид формулы (11) говорит о том, что энтропия S определяется логарифмом числа микросостояний, с помощью которых реализуется макросостояние, которое рассматривается:
\[S=klnГ\ \left(12\right).\]Равенство (12) называется формулой Больцмана. Она позволяет сказать, что чем более упорядочена система, тем меньше количество микросостояний, которыми осуществляется макросостояние. Поэтому говорят, что энтропия -- мера упорядоченности системы. В состоянии равновесия энтропия максимальна.
Энтропия величина аддитивная. Изоэнтропийным называют процесс при S=const. Энтропия физически однородной системы является функцией двух независимых параметров состояния (масса считается постоянной).
Задание: Идеальный газ расширяется изотермически, сравните изменение энтропии, если объем изменяется от $V_1$до $V_2$, температура в первом процессе $T_1$ во втором $T_2$ ($T_2>T_1$).
Решение:
Используя определение энтропии, то, что в идеальном газе процессы обратимы, получим формулу для нахождения $\triangle S$ при $T=const$:
\[\triangle S=\int\limits^{\left(2\right)}_{\left(1\right)}{\frac{\delta Q}{T}}=\frac{1}{T}\int\limits^{\left(2\right)}_{\left(1\right)}{\delta Q}\left(1.1\right).\]Запишем первое начало термодинамики, учитывая, что при $T=const$ $dU=0$:
\[\delta Q=pdV\ \left(1.2\right).\]Из уравнения Менделеева -- Клайперона выразим давление:
\[pV=\nu RT\to p=\frac{\nu RT}{V}\left(1.3\right).\]Подставим (1.3), (1.2) в (1.1), получим:
\[\triangle S=\frac{1}{T}\int\limits^{\left(2\right)}_{\left(1\right)}{\frac{нRT}{V}}dV=\frac{RTн}{T}\int\limits^{\left(2\right)}_{\left(1\right)}{\frac{dV}{V}}=\nu Rln(\frac{V_2}{V_1})(1.4)\]Ответ: Изменение энтропии в изотермическом процессе не зависит от температуры согласно формуле (1.4), следовательно, изменения энтропии для процессов, заданных в условиях задачи равны.
Задание: На рис 1. представлены два обратимых процесса (I и II). Сравните количество теплоты, которую поглощает система в этих процессах.
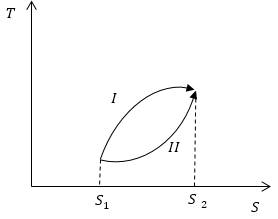
Рис. 1
Решение:
За основу решения примем определение энтропии для обратимых процессов:
\[dS=\frac{\delta Q}{T}\left(2.1\right).\]Выразим $\delta Q\ $из уравнения (2.1), получим:
\[\delta Q=TdS\ (2.2)\]Для того, чтобы определить количество тепла, подведенного к системе, в процессе необходимо проинтегрировать (2.2).
\[\triangle Q=\int\limits^{S_2}_{S_1}{TdS}\ \left(2.3\right).\]Используя геометрическое свойство интеграла (о площади) и рассматривая рис.1, можно сделать вывод, о том, что, так как площадь, ограниченная кривой процесса I осью S и изоэнтропами, проведенными перпендикулярно оси S и проходящими через начало и конец процесса, больше, чем площадь для процесса II, то $Q_I>Q_{II}$.
Ответ: Количество теплоты, которую поглощает система в процессе I больше, чем количество теплоты, которое поглощается в процессе II.












