Поток вектора напряженности поля точечного заряда
Рассмотрим поле точечного заряда $q$, найдем поток вектора напряжённости ($\overrightarrow{E}$) через замкнутую поверхность $S$. Будем считать, что заряд находится внутри поверхности. Поток вектора напряженности через любую поверхность равен количеству линий вектора напряженности, которые выходят наружу (начинаются на заряде, если $q>0$) или количеству линий $\overrightarrow{E}$входящих внутрь, если $q \[Ф_E=\frac{q}{{\varepsilon }_0}\ \left(1\right),\]
где знак потока совпадает со знаком заряда.
Теорема Остроградского - Гаусса в интегральной форме
Допустим, что внутри поверхности S находится N точечных зарядов, величины $q_1,q_2,\dots q_N.$ Из принципа суперпозиции мы знаем, что результирующая напряженность поля всех N зарядов может быть найдена как сумма напряженностей полей, которые создаются каждым из зарядов, то есть:
Следовательно, для потока системы точечных зарядов можно записать:
Используем формулу (1), получаем, что:
Уравнение (4) значит, что поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, которые находятся внутри данной поверхности, деленой на электрическую постоянную. Это теорема Остроградского - Гаусса в интегральной форме. Данная теорема является следствием закона Кулона. Значение данной теоремы заключается в том, что она позволяет довольно просто вычислять электрические поля при различных распределениях зарядов.
Как следствие теоремы Остроградского - Гаусса надо сказать, что поток вектора напряженности ($Ф_E$) через замкнутую поверхность в случае при котором заряды находятся вне данной поверхности, равен нулю.
В том случае, когда можно не учитывать дискретность зарядов используют понятие объемной плотности заряда ($\rho $), если заряд распределен по объему. Она определена как:
\[\rho =\frac{dq}{dV}\left(5\right),\]где $dq$ - заряд, который можно считать точечным, $dV$ -- малый объем. (Относительно $dV$ необходимо сделать следующее замечание. Данный объем мал настолько, чтобы плотность заряда в нем можно было считать постоянной, но достаточно велик, чтобы не начала проявляться дискретность заряда). Суммарный заряд, который находится в полости, можно найти как:
\[\sum\limits^N_{i=1}{q_i\ }=\int\limits_V{\rho dV}\left(6\right).\]В таком случае формулу (4) перепишем в виде:
\[\oint\limits_S{\overrightarrow{E}d\overrightarrow{S}}=\frac{1}{{\varepsilon }_0}\int\limits_V{\rho dV}\left(7\right).\]Теорема Остроградского - Гаусса в дифференциальной форме
Используя формулу Остроградского - Гаусса для любого поля векторной природы, с помощью которой осуществляется переход от интегрирования по замкнутой поверхности к интегрированию по объему:
\[\oint\limits_S{\overrightarrow{a}\overrightarrow{dS}=\int\nolimits_V{div}}\overrightarrow{a}dV\ \left(8\right),\]где $\overrightarrow{a}-$вектор поля (в нашем случае это $\overrightarrow{E}$), $div\overrightarrow{a}=\overrightarrow{\nabla }\overrightarrow{a}=\frac{\partial a_x}{\partial x}+\frac{\partial a_y}{\partial y}+\frac{\partial a_z}{\partial z}$ -- дивергенция вектора $\overrightarrow{a}$ в точке с координатами (x,y,z), которая отображает векторное поле на скалярное. $\overrightarrow{\nabla }=\frac{\partial }{\partial x}\overrightarrow{i}+\frac{\partial }{\partial y}\overrightarrow{j}+\frac{\partial }{\partial z}\overrightarrow{k}$ - оператор набла. (В нашем случае будет $div\overrightarrow{E}=\overrightarrow{\nabla }\overrightarrow{E}=\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}$) -- дивергенция вектора напряженности. Следуя вышесказанному, формулу (6) перепишем как:
\[\oint\limits_S{\overrightarrow{E}\overrightarrow{dS}=\int\nolimits_V{div}}\overrightarrow{E}dV=\frac{1}{{\varepsilon }_0}\int\limits_V{\rho dV}\left(9\right).\]Равенства в уравнении (9) выполняются для любого объема, а это осуществимо только, если функции, которые находятся в подынтегральных выражениях, равны в каждой токе пространства, то есть мы можем записать, что:
Выражение (10) -- теорема Остроградского - Гаусса в дифференциальной форме. Трактовка ее такова: заряды являются источниками электрического поля. Если $div\overrightarrow{E}>0$, то в этих точках поля (заряды положительные) мы имеем источники поля, если $div\overrightarrow{E}
Задание: Заряд равномерно распределен по объему, в этом объеме выделена кубическая поверхность, со стороной b. Она вписана в сферу. Найдите отношение потоков вектора напряженности сквозь эти поверхности.
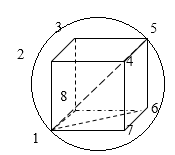
Рис. 1
Решение:
Согласно теореме Гаусса поток ($Ф_E$) вектора напряженности $\overrightarrow{E}$ через замкнутую поверхность при равномерном распределении заряда по объему равен:
\[Ф_E=\frac{1}{{\varepsilon }_0}Q=\frac{1}{{\varepsilon }_0}\int\limits_V{\rho dV=\frac{\rho }{{\varepsilon }_0}\int\limits_V{dV}=\frac{\rho V}{{\varepsilon }_0}}\left(1.1\right).\]Следовательно, нам необходимо определить объемы куба и шара, если шар описать вокруг этого куба. Для начала, объем куба ($V_k$) если сторона его b равен:
\[V_k=b^3\left(1.2\right).\]Найдем объем шара ($V_{sh}$) по формуле:
\[V_{sh}=\frac{1}{6}\pi D^3\left(1.3\right),\]где $D$ -- диаметр шара и (так как шар описан вокруг куба), главная диагональ куба. Следовательно, нам необходимо выразить диагональ куба через его сторону. Это легко сделать, если использовать теорему Пифагора. Для вычисления диагонали куба, например, (1,5) нам сначала необходимо найти диагональ квадрата (нижнего основания куба) (1,6). Длина диагонали (1,6) равна:
\[d_{16}=\sqrt{b^2+b^2\ \ \ }\left(1.4\right),\]В таком случает длина диагонали (1,5) равна:
\[{D=D}_{15}=\sqrt{b^2+{(\sqrt{b^2+b^2\ \ \ })}^2}=b\sqrt{3}\ \left(1.5\right).\]Подставим в (1.3) найденный диаметр шара, получим:
\[V_{sh}=\frac{1}{6}\pi b^3{\left(3\right)}^{\frac{3}{2}}=\frac{\sqrt{3}}{2}\pi b^3\left(1.6\right).\]Теперь мы можем найти потоки вектора напряженности через поверхность куба, она равна:
\[Ф_{Ek}=\frac{\rho V_k}{{\varepsilon }_0}=\frac{\rho b^3}{{\varepsilon }_0}\left(1.7\right),\]через поверхность шара:
\[Ф_{Esh}=\frac{\rho V_{sh}}{{\varepsilon }_0}=\frac{\rho }{{\varepsilon }_0}\frac{\sqrt{3}}{2}\pi b^3\ \left(1.8\right).\]Найдем отношение $\frac{Ф_{Esh}}{Ф_{Ek}}$:
\[\frac{Ф_{Esh}}{Ф_{Ek}}=\frac{\frac{с}{\varepsilon_0}\frac{\sqrt{3}}{2} \pi b^3}{\frac{сb^3}{\varepsilon_0}}=\frac{\pi}{2}\sqrt{3}\ \approx 2,7\left(1.9\right).\]Ответ: Поток через поверхность шара в 2,7 раза больше.
Задание: Докажите, что заряд проводника располагается на его поверхности.
Решение:
Используем для доказательства теорему Гаусса. Выделим в проводнике замкнутую поверхность произвольной формы около поверхности проводника (рис.2).
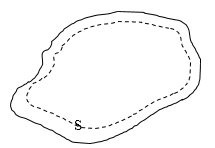
Рис. 2
Допустим, что заряды внутри проводника есть, запишем с теорему Остроградского - Гаусса для дивергенции поля имеем для любой точки поверхности S:
\[div\overrightarrow{E}=\frac{1}{{\varepsilon }_0}\rho \left(2.1\right),\]где $\rho -плотность\ $внутреннего заряда. Однако поля внутри проводника нет, то есть $\overrightarrow{E}=0$, следовательно, $div\overrightarrow{E}=0\to \rho =0$. Теорема Остроградского - Гаусса в дифференциальной форме локальна, то есть, она записана для точки поля, мы специальным образом точку не выбирали, следовательно, плотность заряда равна нулю в любой точке поля внутри проводника.












