Статика - раздел механики, в котором изучают условия равновесия материальных тел под действием сил. К основным понятиям статики относятся понятия о силе, моменте силы относительно центра или относительно оси вращения и о паре сил.
Основная задача статики состоит в определении условий, при которых тело, на которое действуют силы, может оставаться в покое. Кроме того, статика дает указание о направлении движения тела, если его равновесие нарушено действием определенной силы.
В основе статики лежат принципы, которые являются следствием основных законов механики. Они отражают свойства сил, действующих на материальную точку и абсолютно твердое тело.
Принципы статики
- Сила в механике является вектором. Поэтому если на тело действует несколько сил, то их можно заменить одной равнодействующей силой, равной геометрической сумме действующих сил.
- Силы можно складывать и вычитать в соответствии с правилами сложения и вычитания векторов.
- Точку приложения силы можно переносить вдоль ее направления, не меняя действие силы на тело в целом. На рис. 1.а. в точках A и В на тело действуют равные силы f1 и f2 противоположного направления. В теле возникает деформация и появляются упругие силы f3 и f4. Как показано на рис. 1.б., при перенесении силы f1 из точки А в точку А' равновесие не нарушается.
- Силу можно разложить на составляющие, т. е. определить силы, равнодействующая которых известна. На рис. 2 сила F разложена на составляющие F1 и F2 вдоль заданных направлений АВ и АС.
- Правило рычага: если линии действия сил F1 и F2 не пересекаются, то их равнодействующая F делит расстояние между этими силами l = l1 + l2 в отношении, обратном отношению сил (рис.3): $\frac{F_1}{F_2}=\frac{l_2}{l_1}$
- Момент силы: сила действующая на тело, ззакреплённое на оси, может вызвать его вращение только в том случае, когда направление силы не проходит через ось вращения. Говорят,
что сила, которая вызывает такое вращение тела, создает момент силы. Момент силы $\overrightarrow{M}o(\overrightarrow{F})$ равен векторному произведению вектора положения $
\overrightarrow{r}$, проведенного из точки О на оси вращения до места приложения силы F, на вектор этой силы (рис. 4):
\[\overrightarrow{M}o\left(\overrightarrow{F}\right)=\overrightarrow{r}\times \overrightarrow{F}\]
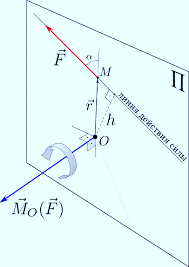
Рисунок 4. Момент вращения
Момент силы равен произведению модуля силы F на расстояние h от оси вращения до линии, вдоль которой действует сила:
$\left|\overrightarrow{M}o\left(\overrightarrow{F}\right)\right|=Fh=Fr{sin {\mathbf \alpha }\ }$, где ${\mathbf \alpha }$ --- угол между векторами $\overrightarrow{r}$ и $ \overrightarrow{F}$.
Расстояние h называется плечом силы. Момент силы есть аксиальный вектор, он направлен вдоль оси вращения в соответствии с правилом правого винта (или правилом буравчика).
Единицей момента силы в СИ является ньютон на метр: $\left|\overrightarrow{M}o\right|=н\cdot м\ $.
Если на тело действует п сил, то результирующий момент равен геометрической сумме моментов составляющих сил. Сила, момент которой относительно данной оси равен нулю, не вызывает вращения вокруг этой оси.
- Действие момента силы аналогично действию пары сил. Парой сил называются такие две силы, равнодействующая которых равна нулю, а результирующий момент относительно какой-либо оси не равен нулю. Если тело закреплено на оси, то при действии на него пары сил оно начнет вращаться вокруг этой оси. Момент пары сил относительно любой оси, перпендикулярной плоскости пары (рис. 5), одинаков, и определяется соотношением $\overrightarrow{M}\left(\overrightarrow{F},\overrightarrow{F'}\ \right)=\overrightarrow {M}\left(\overrightarrow{F}\right)+\overrightarrow{M}\left(\overrightarrow{F'}\ \right);;\ \left|\overrightarrow{M}\left(\overrightarrow{F},\overrightarrow{F'}\ \right)\right| =Fh=F\left|AB\right|{sin {\mathbf \alpha }\ }$. Расстояние h называется плечом пары сил.
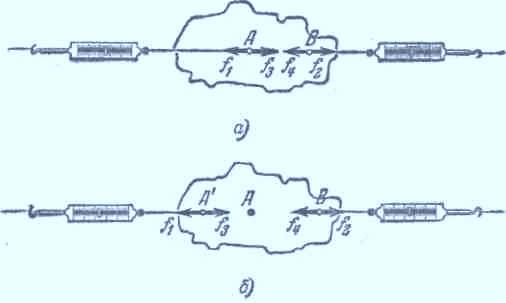
Рисунок 1. Перенос точки приложения силы
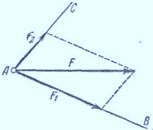
Рисунок 2. Разложение силы на составляющие
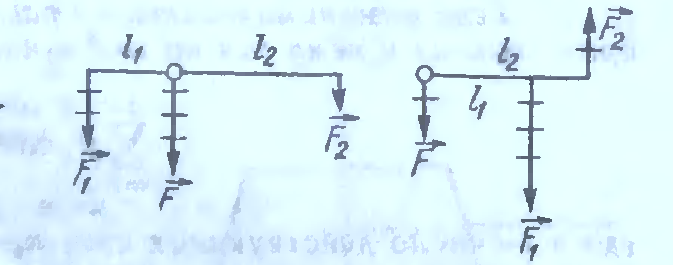
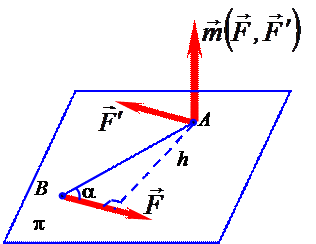
Рисунок 5. Момент пары сил
На рис.2 вектор $\overrightarrow{F}$ разложен на взаимно перпендикулярные составляющие ${\overrightarrow{F}}_1$ и ${\overrightarrow{F}}_2$. Угол между векторами $\alpha = \widehat{\overrightarrow{F}\ {\overrightarrow{F}}_2}=60{}^\circ $. $\overrightarrow{F}=10\ Н$. Найти ${\overrightarrow{F}}_1$ и ${\overrightarrow{F}}_2$
Решение
\[{\overrightarrow{F}}_2=\overrightarrow{F}{cos \alpha \ }=10\cdot \frac{1}{2}=5\ Н;;\ \ \ \ \ \ {\overrightarrow{F}}_2=\overrightarrow{F}{cos \left(90-\alpha \right)\ }= \overrightarrow{F}{sin \alpha \ }=10\cdot \frac{\sqrt{3}}{2}=8,67\ Н\]На рис. 5 момент пары сил, приложенных к точкам А и В, $\left|\overrightarrow{M}\left(\overrightarrow{F},\overrightarrow{F'}\ \right)\right|=12\ Н\cdot м$. Расстояние между точками приложения сил -- 6 м. Угол $\alpha =30{}^\circ $. Найти, какая сила приложена в каждой из точек.
Решение
\[\left|\overrightarrow{M}\left(\overrightarrow{F},\overrightarrow{F'}\ \right)\right|=F\left|AB\right|{sin \alpha \ }\] \[ F=F'=\frac{\overrightarrow{M}\left(\overrightarrow{F},\overrightarrow{F'}\ \right)}{\left|AB\right|{sin \alpha \ }}=\frac{12}{6\cdot \frac{1}{2}}=4\ Н\ \ \ \]











