Подвижный блок отличается от неподвижного тем, что его ось не закреплена, и он может подниматься и опускаться вместе с грузом.
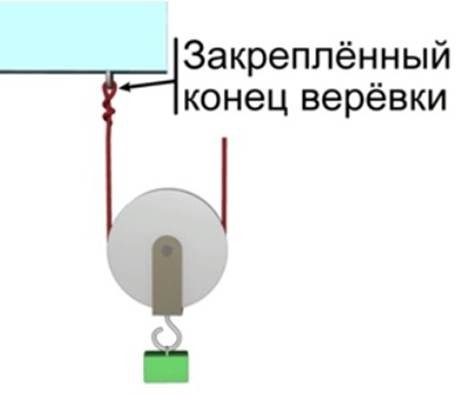
Рисунок 1. Подвижный блок
Как и неподвижный блок, подвижный блок состоит всё из того же колеса с желобом для троса. Однако здесь закреплен один конец троса, а колесо подвижно. Колесо движется вместе с грузом.
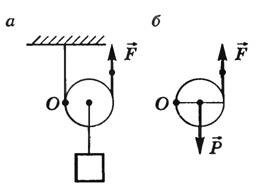
Рисунок 2. Силы и плечи сил в подвижном блоке
Подвижный блок перемещается вместе с грузом, он как бы лежит на веревке. В таком случае точка опоры в каждый момент времени будет находиться в месте соприкосновения блока с веревкой с одной стороны, воздействие груза будет приложено к центру блока, где он и крепится на оси, а сила тяги будет приложена в месте соприкосновения с веревкой с другой стороны блока. То есть плечом веса тела будет радиус блока, а плечом силы нашей тяги -- диаметр. Правило моментов в этом случае будет иметь вид:
$$mgr = F \cdot 2r \Rightarrow F = mg/2$$Таким образом, подвижный блок дает выигрыш в силе в два раза.
Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис. 3). Неподвижный блок применяется только для удобства. Он, изменяет направление действия силы, позволяет, например, поднимать груз, стоя на земле, а подвижный блок обеспечивает выигрыш в силе.
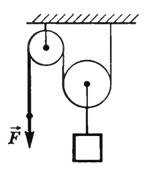
Рисунок 3. Комбинация неподвижного и подвижного блоков
Мы рассмотрели идеальные блоки, то есть такие, в которых не учитывалось действие сил трения. Для реальных же блоков необходимо вводить поправочные коэффициенты. Используют такие формулы:
Неподвижный блок
$F = f • mg $
Подвижный блок
$F = f • 1/2 mg $
В этих формулах: $F$ - прилагаемое внешнее усилие (обычно это сила рук человека), $m$ - масса груза, $g$ - коэффициент силы тяжести, $f$ - коэффициент сопротивления в блоке (для цепей примерно 1,05, а для верёвок 1,1).
С помощью системы из подвижного и неподвижного блоков грузчик поднимает ящик с инструментами на высоту $S_1$ = 7 м, прикладывая силу $F$ = 160 Н. Какова масса ящика, и сколько метров верёвки придётся выбрать, пока груз поднимется? Какую работу выполнит в результате грузчик? Сравните её с работой, выполненной над грузом по его перемещению. Трением и массой подвижного блока пренебречь.
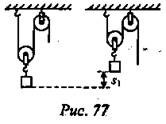
Решение
Дано:
$F$ = 160 H
$S_1$ = 7 м
$m, S_2 , A_1 , A_2$ - ?
Подвижный блок даёт двойной выигрыш в силе и двойной проигрыш в перемещении. Неподвижный блок не даёт выигрыша в силе, но меняет её направление. Таким образом, приложенная сила будет вдвое меньше веса груза: $F = 1/2P = 1/2mg$, откуда находим массу ящика: $m=\frac{2F}{g}=\frac{2\cdot 160}{9,8}=32,65\ кг$
Перемещение груза будет вдвое меньше, чем длина выбранной верёвки:
\[S_2=2S_1=2\cdot 7=14\ м\]Выполненная грузчиком работа равна произведению приложенного усилия на перемещение груза: $A_2=F\cdot S_2=160\cdot 14=2240\ Дж\ $.
Работа, выполненная над грузом:
\[A_1=mgS_1=32,65\cdot 9,8\cdot 7=2240\ Дж\]Ответ: Масса ящика 32,65 кГ. Длина выбранной верёвки 14 м. Выполненная работа равна 2240 Дж и не зависит от способа подъёма груза, а только от массы груза и высоты подъёма.
Какой груз можно поднять с помощью подвижного блока весом 20 Н, если тянуть веревку с силой 154 Н?
Решение
Дано:
$Р_Б$ = 20 Н
$F$ = 154 H
$f$ = 1,1
$P$ - ?
Запишем правило моментов для подвижного блока: $F = f • 1/2 (P+ Р_Б)$, где $f$ - поправочный коэффициент для верёвки.
Тогда $P=2\frac{F}{f}-P_Б=2\cdot \frac{154}{1,1}-20=260\ Н$
Ответ: Вес груза 260 Н.











