Наклонная плоскость представляет собой плоскую поверхность, расположенную под тем или иным углом к горизонтали. Она позволяет поднять груз с меньшей силой, чем если бы этот груз поднимался вертикально вверх. На наклонной плоскости груз поднимается вдоль этой плоскости. При этом он преодолевает большее расстояние, чем если бы поднимался вертикально.
Причем во сколько раз происходит выигрыш в силе, во столько раз будет больше расстояние, которое преодолеет груз.
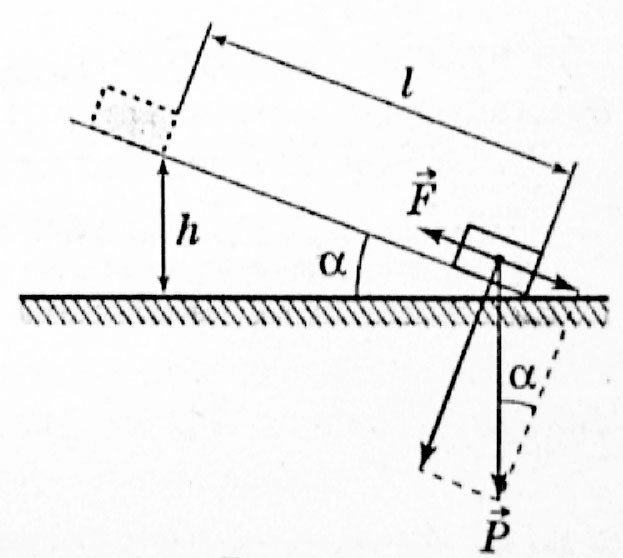
Рисунок 1. Наклонная плоскость
Если высота, на которую надо поднять груз, равна $h$, и при этом затрачивалась бы сила $F_h$, а длина наклонной плоскости $l$, и при этом затрачивается сила $F_l$, то $l$ так относится к $h$, как $F_h$ относится к $F_l$: $l/h = F_h/F_l$... Однако $F_h$ - это вес груза ($P$). Поэтому обычно записывают так: $l/h = P/F$, где $F$ - сила, поднимающая груз.
Величина силы $F$, которую надо приложить к грузу весом $Р$, чтобы тело находилось в равновесии на наклонной плоскости, равна $F_1 = Р_h/l = Рsin{\mathbf \alpha }$, если сила $Р$ приложена параллельно наклонной плоскости (рис.2, а), и $F_2$ = $Р_h/l = Рtg{\mathbf \alpha }$, если сила $Р$ приложена параллельно основанию наклонной плоскости (рис.2, б).
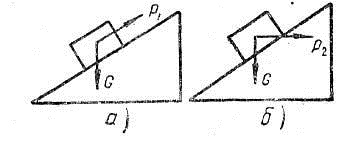
Рисунок 2. Движение груза по наклонной плоскости
а) сила параллельна плоскости б) сила параллельна основанию
Наклонная плоскость дает выигрыш в силе, с ее помощью можно легче поднять груз на высоту. Чем меньше угол $\alpha $, тем больше выигрыш в силе. Если угол $\alpha $ меньше угла трения, то груз самопроизвольно не будет двигаться, и нужно усилие, чтобы тянуть его вниз.
Если учесть силы трения между грузом и наклонной плоскостью, то для $F_1$ и $F_2$ получаются следующие значения: $F_1=Рsin($${\mathbf \alpha }$$\pm$${\mathbf \varphi }$)/cos${\mathbf \varphi }$; $F_2=Рtg($${\mathbf \alpha }$$\pm$${\mathbf \varphi }$)
Знак плюс относится к передвижению вверх, знак минус - к опусканию груза. Коэффициент полезного действия наклонной плоскости ${\mathbf \eta }$1=sin${\mathbf \alpha }$cos${\mathbf \alpha }$/sin(${\mathbf \alpha }$+${\mathbf \varphi }$), если сила $Р$ направлена параллельно плоскости, и ${\mathbf \eta }$2=tg${\mathbf \alpha }$/tg(${\mathbf \alpha }$+${\mathbf \varphi }$), если сила $Р$ направлена параллельно основанию наклонной плоскости.
Наклонная плоскость подчиняется «золотому правилу механики». Чем меньше угол между поверхностью и наклонной плоскостью (т. е. чем она более пологая, не круто поднимающаяся вверх), тем меньше надо прикладывать сил для подъема груза, но и большее расстояние необходимо будет преодолеть.
При отсутствии сил трения выигрыш в силе $K = P/F = 1/sin$$\alpha = l/h$. В реальных условиях из-за действия силы трения КПД наклонной плоскости меньше 1, выигрыш в силе меньше отношения $l/h$.
Груз массой 40 кг поднимают по наклонной плоскости на высоту 10 м при этом прикладывая силу 200 Н (рис.3). Какова длина наклонной плоскости? Трением пренебречь.
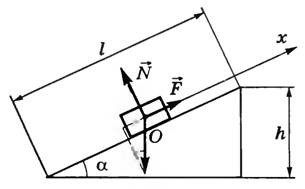
Рисунок 3
Решение
Дано:
$F$ = 200 H
$m$ = 40 кг
$H$ = 10 м
${\mathbf \eta }$ = 1
$g$ = 9.8 м/c2
$m$ - ?
При движении тела по наклонной плоскости отношение прилагаемой силы к весу тела равно отношению длины наклонной плоскости к её высоте: $\frac{F}{P}=\frac{l}{h}=\frac{1}{{sin {\mathbf \alpha }\ }}$. Следовательно, $l=\frac{Fh}{mg}=\ \frac{200\cdot 10}{40\cdot 9,8}=5,1\ м$.
Ответ: Длина наклонной плоскости 5,1 м
Два тела с массами $m_1$ = 10 г и $m_2$ = 15 г связаны нитью, перекинутой через неподвижный блок, установленный на наклонной плоскости (рис. 4). Плоскость образует с горизонтом угол $\alpha $ = 30${}^\circ$. Найти ускорение, с которым будут двигаться эти тела.
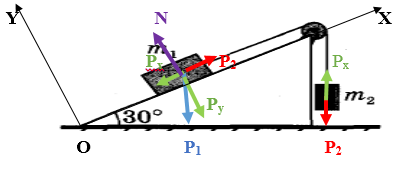
Решение
Дано:
$m_1$ = 10 Г
$m_2$ = 15 Г
${\mathbf \alpha }$ = 30 градусов
$g$ = 9.8 $м/c_2$
$m$ - ?
Направим ось ОХ вдоль наклонной плоскости, а ось ОY - перпендикулярно ей, и спроектируем на эти оси вектора $\ {\overrightarrow{Р}}_1\ и\ {\overrightarrow{Р}}_2$. Как видно из рисунка, равнодействующая сил, приложенных к каждому из тел, равна разности проекций векторов $\ {\overrightarrow{Р}}_1\ и\ {\overrightarrow{Р}}_2$ на ось ОХ:
\[\left|\overrightarrow{R}\right|=\left|P_{2x}-P_{1x}\right|=\left|m_2g{sin \alpha \ }-m_1g{sin \alpha \ }\right|=g{sin \alpha \left|m_2-m_1\right|\ }\] \[\left|\overrightarrow{R}\right|=9.8\cdot {sin 30{}^\circ \ }\cdot \left|0.015-0.01\right|=0.0245\ H\] \[a_1=\frac{R}{m_1}=\frac{0.0245}{0.01}=2,45\frac{м}{с^2};\ \ \ \ \ \ a_2=\frac{R}{m_2}=\frac{0.0245}{0.015}=1,63\ м/с^2\]Ответ: Ускорения тел $a_1=2,45\frac{м}{с^2};\ \ \ \ \ \ a_2=1,63\ м/с^2$











