Эмпирический способ нахождения скорости электромагнитных волн
Скорость распространения электромагнитных волн эмпирически определяют, изучая стоячие волны, которые получают, например, в цепи, которая изображена на рис. 1, где выход генератора соединен с проводами линии через конденсаторы. Когда генератор работает, между проводами появляются колебания напряжения, а, значит, существуют колебания электрического поля, то есть возникает электромагнитная волна.
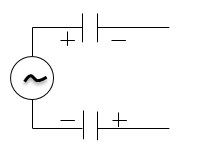
Рисунок 1.
Для понимания об интенсивности колебаний в различных точках линии включают лампы накаливания. В таких опытах можно показать, что стоячие волны в линии появляются только при определенной частоте генератора, когда она совпадает с частотой собственных колебаний линии.
Измеряя расстояния ($\triangle x$) между соседними узлами или пучностями в стоячей волне, определяется $\frac{1}{2}$ длины волны ($\lambda $). При этом, известно, что:
где $\nu $ -- частота генератора. Измерив $\nu $, легко найти скорость распространения электромагнитной волны. Опыты показали, что скорость электромагнитной волны ($v$) совпадает со скоростью света. В воздухе она приблизительно равна $v=c=3\cdot {10}^8\frac{м}{с}.$
Вывод скорости распространения электромагнитных волн из теории Максвелла
Раньше, чем электромагнитные волны были получены в экспериментах, Максвелл вычислил скорость этих волн, используя свою теорию поля. Рассмотри плоскую электромагнитную волну (одномерная задача, означающая, что $\overrightarrow{E\ }и\ \overrightarrow{H\ }зависят\ только\ от\ одной\ координаты,\ допустим\ x$), которая распространяется в однородной среде ($j_x=j_y=j_z=0,\ при\ \varepsilon =const,\ \mu =const$). В таком случае система уравнений Максвелла в скалярном виде будет записана как:
Исключим из уравнений Максвелла электрическое поле. С этой целью используем формулу, связывающую индукцию магнитного поля и его напряженность:
и продифференцируем второе уравнение системы (2) по времени, получим:
Первое уравнение системы (2) продифференцируем по $x$, и используем уравнение:
в результате имеем:
Сравним уравнения (4) и (6), запишем:
Уравнение (7) есть волновое уравнение, следовательно, коэффициент, который стоит при $\frac{{\partial }^2H}{\partial x^2}$ - квадрат скорости распространения электромагнитной волны:
$c$- скорость света. В вакууме скорость электромагнитных волн будет выражена как:
Теория Максвелла предсказала, что скорость распространения электромагнитных волн в вакууме равна скорости света - этот факт доказывает, что свет имеет электромагнитную природу.
Основные процессы при распространении волн в проводах происходят не внутри проводов, а в окружающей их среде. Следовательно, если среда вне провода изменится, то скорость электромагнитных волн будет другой, длина волны при неизменной частоте генератора станет другой.
В справедливости формулы (8) легко убедиться на опыте, если часть двухпроводной линии, которая первоначально была в воздухе погрузить в воду. Для воды $\mu \approx 1,\ \varepsilon >1,$ следовательно, скорость электромагнитных волн в воде меньше, чем в воздухе, значит расстояние между соседними узлами (пучностями) станет меньше.
Следует учитывать, что $\mu \ и\ \ \varepsilon $ зависят от частоты. Поэтому при нахождении скорости применяя формулу (8) следует использовать их значения, соответствующие частоте колебаний в электромагнитной волне.
Задание: Параллельные провода (рис.2) находятся в некотором веществе, магнитная проницаемость которого равна $1$, диэлектрическая проницаемость не равна $1$. Они посредством индуктивности соединены с генератором. При высокой частоте колебаний $\nu $ в системе устанавливаются стоячие электромагнитные волны. Вдоль проводов перемещают газоразрядную трубку $А$, по интенсивности ее свечения определили положения пучностей напряженности электрического поля, расстояние между которыми оказались равны $\triangle x$. Какова диэлектрическая проницаемость вещества?
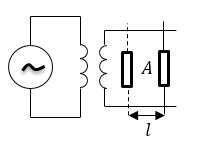
Рисунок 2.
Решение:
Стоячие электромагнитные волны появляются как результат интерференции волн, которые распространяются по двухпроводной линии от генератора в прямом направлении с волнами, которые отражаются концами линии. При высокой частоте электромагнитных колебаний основные процессы, которые связаны с распространением волн, происходят в среде, которая окружает провода.
В соответствии с теорией Максвелла скорость электромагнитных волн в среде равна:
\[v=\frac{c}{\sqrt{\varepsilon \mu }}\left(1.1\right).\]По условию задачи для данного вещества $\mu =1$, диэлектрическая проницаемость выразится из (1.1) как:
\[\varepsilon =\frac{c^2}{v^2}\left(1.2\right).\]Скорость электромагнитных волн связана с длинной волны как:
\[v=\lambda \nu \left(1.3\right).\]Расстояние между соседними пучностями в стоячей волне равно половине длины волны ($\triangle x=\frac{1}{2}\lambda $), в таком случае имеем:
\[\varepsilon =\frac{c^2}{{(\lambda \nu )}^2}=\frac{c^2}{{4\triangle x^2\nu }^2}.\]Ответ: $\varepsilon =\frac{c^2}{{4\triangle x^2\nu }^2}.$
Задание: Какова скорость распространения электромагнитной волны в концентрическом кабеле, в котором пространство между внешним и внутренним проводами заполнено диэлектриком с проницаемостью $\varepsilon ?$ Считайте, что потерями в кабеле можно пренебречь.
Решение:
Согласно теории Максвелла, скорость распространения электромагнитных волн в веществе равна:
\[v=\frac{c}{\sqrt{\varepsilon \mu }}\left(2.1\right).\]Магнитную проницаемость среды можно считать равной единице, тогда выражение (2.1) перепишем в виде:
\[v=\frac{c}{\sqrt{\varepsilon }}.\]Ответ: $v=\frac{c}{\sqrt{\varepsilon }}.$












