Циркуляция произвольного вектора
Работу, совершаемую силами электрического поля, по перемещению заряда $q$ на расстояние $ds$ найдем как:
Если заряд перемещается по конечному пути $L$ работа равна:
где необходимо подынтегральное выражение просуммировать для всех элементарных участков L. Такая операция - интегрирование по линии $L$.
Работа сил электростатического поля
Работа может зависеть, в общем случае, как от положения начала и окончания пути, так и формы пути. Однако электрическое поле статичных зарядов обладает такой особенностью, что работа его сил на пути между двумя произвольными точками зависит только от положения этих точек и не зависит о формы пути. Силовые поля, которые обладают таким свойством, называют потенциальными или консервативными. От сюда следует, что работа консервативного поля на любом замкнутом пути равна нулю. Вообще говоря, поле произвольного вектора $\overrightarrow{A}$ (не зависимо от его физического смысла) является потенциальным полем только в том случае, если при всяком выборе замкнутого пути интегрирования выполняется равенство:
Интеграл, представленный в левой части уравнения (3), называют циркуляцией некоторого произвольного вектора $\overrightarrow{A}$ вдоль пути $L$. Таким образом, получаем, что циркуляция вектора напряженности по любому замкнутому контуру равна нулю:
Из условия (4) для вектора напряженности поля следует, непрерывность тангенциальных составляющих напряженности (в отличие от нормальных составляющих). Это значит, что компоненты напряженности, которые являются касательными к выбранной любой поверхности во всякой ее точке, имеют по обе стороны поверхности равные значения.
Рассмотрим работу (dA) сил электростатического поля по перемещению элементарного заряда $dq$ на малом отрезке $ds$. Она равна:
где $dr$ -- проекция перемещения пробного заряда на радиус-вектор $\overrightarrow{r}$, который провели из заряда (Q) - источника поля. Из уравнения (4) следует, что работа, которую совершает поле, при перемещении заряда $q$ из точки $R_1\ в\ точку\ R_2\ $по пути $L$ равна:
Мы получили, что работа сил электростатического поля зависит только от конечного и начального положений точек пути, не зависит от его формы. Следовательно, поле неподвижного точечного заряда консервативно. Сумма потенциальных полей есть также консервативное поле, следовательно, работа результирующего поля не будет зависеть от формы пути. Интегральное условие потенциальности поля (3) можно преобразовать в дифференциальное:
Или для вектора напряженности имеем:
Напомним, что $rot\ \overrightarrow{E}=\overrightarrow{\nabla }\times \overrightarrow{E}=\left| \begin{array}{ccc} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ E_x & E_y & E_k \end{array} \ \right|.$
Задание: Точечные заряды $q_1$ и $q_2$ находятся на расстоянии $r_1$ друг от друга. Какую работу надо совершить силам поля, чтобы второй заряд оттолкнулся от первого и удалился на бесконечность?
Решение:
Работа, которую совершает поле по перемещению точечного заряда, равна:
\[A=-kq_1q_2\left(\frac{1}{R_2}-\frac{1}{R_1}\right)\left(1.1\right).\]Если второй заряд перемещается на бесконечность, то выражение для работы поля примет следующий вид:
\[A=-kq_1q_2\left(-\frac{1}{R_1}\right)=kq_1q_2\frac{1}{R_1}.\]Ответ: Работа сил поля равна $A=kq_1q_2\frac{1}{R_1}.$
Задание: Поле создается двумя одноименно заряженными бесконечными длинными нитями (линейная плотность заряда равна $\tau $), расстояние между нитями равно $d_1$. Найдите, работу на единицу длины ($A_l$), которую необходимо совершить, чтобы сдвинуть нити до расстояния $d_2$ (рис.1).
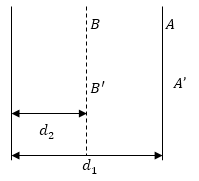
Рис. 1
Решение:
Допустим, что одна нить остается неподвижной, двигаем только правую нить. Она перемещается из положения $AA'$ в положение $ВВ'$. Для того, чтобы уменьшить расстояние между нитями необходимо совершить работу против сил поля ($A'$), так как мы помним, что нити одноименно заряжены и, следовательно, они отталкиваются. Такая работа будет равна по модулю и противоположна по знаку работе сил поля($A$).
В качестве основы для решения используем формулу, которая определяет работу поля:
\[A=\int\limits_L{q}\overrightarrow{E}\cdot d\overrightarrow{s}\ \left(2.1\right).\]Перепишем формулу для работы применительно к условиям задачи:
\[A=-A'=-\int\limits^{d_2}_{d_1}{qE\ \left(x\right)}\cdot dx\ \left(2.2\right),\]где q-заряд нити, которую перемещают в поле, значит это заряд правой нити, который можно найти, зная линейную плотность распределения заряда, а именно:
\[q=\tau l\ \left(2.3\right),\]где l -- длина нити.
В формуле (2.2) $E\ \left(x\right)$ -- напряженность поля, которое создает левая нить (стационарная) и она равна (поле бесконечно длинной нити):
\[E\ \left(x\right)=\frac{\tau }{2\pi {\varepsilon }_0x}\left(2.4\right).\]Подставляем (2.3) и (2.4) в формулу (2.2), получим:
\[A=-\int\limits^{d_2}_{d_1}{\tau l\frac{\tau }{2\pi {\varepsilon }_0x}}\cdot dx=-\frac{l{\tau }^2}{2\pi {\varepsilon }_0}\int\limits^{d_2}_{d_1}{\frac{dx}{x}}=-\frac{l{\tau }^2}{2\pi {\varepsilon }_0}{ln \left(\frac{d_2}{d_1}\right)\ }\left(2.5\right).\]Так как нам в задаче требуется найти работу на единицу длины, то разделим получившийся результат на длину нити (l), получим:
\[A_l=\frac{A}{l}=\frac{{\tau }^2}{2\pi {\varepsilon }_0}{ln \left(\frac{d_1}{{\ d}_2}\right).\ }\]Ответ: Работа будет равна: $A_l=\frac{{\tau }^2}{2\pi {\varepsilon }_0}{ln \left(\frac{d_1}{{\ d}_2}\right)\ }$












