Продольные волны
Продольная волна - волна, в которой колебания происходят в направлении ее распространения. Примером продольной волны может служить звуковая волна.
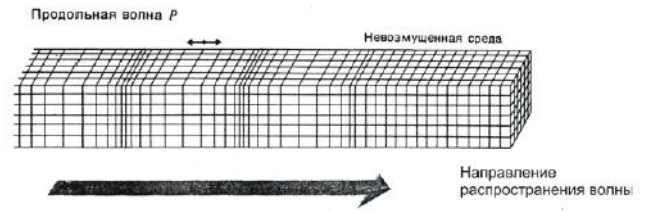
Рисунок 1. Продольная волна
Механические продольные волны также называют компрессионными волнами или волнами сжатия, так как они производят сжатие при движении через среду. Поперечные механические волны также называют "Т-волны" или "волны сдвига".
Продольные волны включают в себя акустические волны (скорость частиц, распространяющихся в упругой среде) и сейсмические Р-волны (созданные в результате землетрясений и взрывов). В продольных волнах, смещение среды параллельно направлению распространения волны.
Звуковые волны
В случае продольных гармонических звуковых волн, частота и длина волны может быть описана формулой:
где
$y_0-$ амплитуда колебаний;\textit{}
$\omega -$ угловая частота волны;
$c-$ скорость волны.
Обычная частота $\left({\rm f}\right)$волны задается
Скорость звука распространения зависит от типа, температуры и состава среды, через которую он распространяется.
В упругой среде, гармоническая продольная волна проходит в положительном направлении вдоль оси.
Поперечные волны
Поперечная волна - волна, в которой направление молекул колебаний среды перпендикулярно к направлению распространения. Примером поперечных волн служит электромагнитная волна.
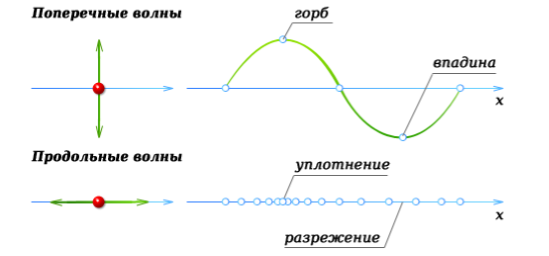
Рисунок 2. Продольная и поперечная волны
Рябь в пруду и волны на струне легко представить в виде поперечных волн.
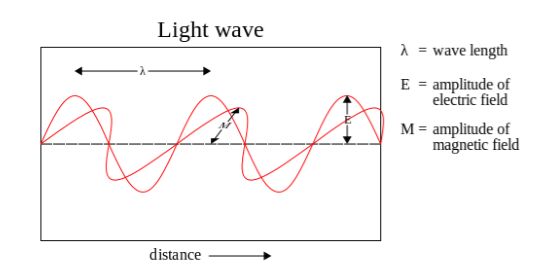
Рисунок 3. Световые волны являются примером поперечной волны
Поперечные волны являются волнами, которые колеблются перпендикулярно к направлению распространения. Есть два независимых направления, в которых могут возникать волновые движения.
Двумерные поперечные волны демонстрируют явление, называемое поляризацией.
Электромагнитные волны ведут себя таким же образом, хотя это немного сложнее увидеть. Электромагнитные волны также являются двухмерными поперечными волнами.
Докажите, что уравнение плоской незатухающей волны ${\rm y=Acos}\left(\omega t-\frac{2\pi }{\lambda }\right)x+{\varphi }_0$ для волны, которая представлена на рисунке, можно записать в виде ${\rm y=Asin}\left(\frac{2\pi }{\lambda }\right)x$. Убедитесь в этом, подставив значения координаты$\ \ x$, которые раны $\frac{\lambda}{4}$; $\frac{\lambda}{2}$; $\frac{0,75}{\lambda}$.
Решение:
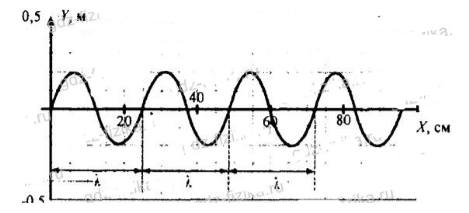
Рисунок 4.
Уравнение $y\left(x\right)$ для плоской незатухающей волны не зависит от $t$, значит, момент времени $t$ можно выбрать произвольным. Выберем момент времени $t$ таким, что
\[\omega t=\frac{3}{2}\pi -{\varphi }_0\] \[t=\frac{\frac{3}{2}\pi -{\varphi }_0}{\omega }\]\end{enumerate}
Подставим это значение в уравнение:
\[y=Acos\left(\omega t-\left(\frac{2\pi }{\lambda }\right)x+{\varphi }_0\right)\]Получим
\[y=Acos\left(\frac{3}{2}\pi -{\varphi }_0-\left(\frac{2\pi }{\lambda }\right)x+{\varphi }_0\right)=Acos\left(\frac{3}{2}\pi -\left(\frac{2\pi }{\lambda }\right)x\right)=\] \[=Acos\left(2\pi -\frac{\pi }{2}-\left(\frac{2\pi }{\lambda }\right)x\right)=Acos\left(2\pi -\left(\left(\frac{2\pi }{\lambda }\right)x+\frac{\pi }{2}\right)\right)=\] \[=Acos\left(\left(\frac{2\pi }{\lambda }\right)x+\frac{\pi }{2}\right)=Asin\left(\frac{2\pi }{\lambda }\right)x\] \[x=\frac{\lambda }{4}=6,25см,\ \ \ \ y=Asin\frac{\pi }{2}=0,2sin\frac{\pi }{2}=0,2\ \] \[x=\frac{\lambda }{2}=12,5\ см,\ \ \ y=0,2*sin\pi =0\] \[{\mathbf x}{\mathbf =}\frac{{\mathbf 3}}{{\mathbf 4}}{\mathbf \lambda }{\mathbf =}{\mathbf 18},{\mathbf 75}{\mathbf \ см,\ \ \ }{\mathbf y}{\mathbf =\ }{\mathbf 0},{\mathbf 2}{\cdot}{\mathbf sin}\frac{{\mathbf 3}}{{\mathbf 2}}{\mathbf \pi }{\mathbf =-}{\mathbf 0},{\mathbf 2}\]Ответ: $Asin\left(\frac{2\pi }{\lambda }\right)x$












