
Принцип тождественности микрочастиц
Все однотипные микрочастицы (электроны, протоны, нейтроны и т.д.) имеют абсолютно идентичные свойства. У них одинаковые массы, электрические заряды, спины и т.д. В этой связи появляется вопрос о том, как проводить отличии одной частицы от другой подобной. Рассмотрим систему из двух электронов. Отметим в начальный момент наблюдения положения данных частиц. Каждому присвоим номер ($1$) и ($2$). В классической физике мы бы сказали, что электрон перемещается по определенной траектории. За движением электрона можно проследить. Зная положение частицы, в какой -- то момент времени, можно сказать, где она будет находиться позднее и определить какой это электрон (номер $1$ или номер $2$). Если мы поменяем местами и скоростями оба электрона, получаем новое состояние системы. При этом новое состояние будет иметь те же свойства, что и первое, за исключением нумерации электронов. В классической интерпретации одинаковые частицы принципиально различимы (индивидуализированы).
В квантовой физике ситуация иная. Так как она отвергает классическое представление о движении частицы по траектории. Состояние системы частиц в квантовой механике описывается волновой функцией, которая имеет вероятностное толкование. В примере, относительно двух электронов, волновая функция зависит от времени и координат обоих электронов. Обнаруживая в момент времен $t$ один из электронов, принципиально невозможно решить какой из присвоенных номеров имеет электрон. Принципиальная невозможность решения вопроса означает, что сам вопрос сформулирован неверно. Если два исследуемых электрона поменять местами, то результат обмена нельзя детектировать. Значит, два состояния, которые эмпирически неразличимы, следует рассматривать как одно и то же состояние. Так поступают в квантовой физике.
Одинаковые частицы в квантовой механике принципиально неразличимы (обезличены). Следует говорить о состоянии системы одинаковых частиц в единстве, а не о состоянии отдельной частицы. Данное утверждение формулируют в виде принципа тождественности одинаковых частиц:
В системе из одинаковых микрочастиц выполняются только состояния, которые не изменяются при перестановке местами двух любых частиц.
Данный принцип в квантовой физике является новым и не вытекает из других ее положений, но можно показать, что он не противоречит всему ранее сказанному. Данный принцип подтверждается эмпирически.
Волновые функции, удовлетворяющие принципу тождественности
Как известно, состояние системы микрочастиц в квантовой физике описывают при помощи волновых функций. Резонным является вопрос о том, какие волновые функции удовлетворяют принципу тождественности одинаковых частиц. Вернемся к рассмотрению системы из двух одинаковых частиц. Допустим, что волновая функция от времени не зависит и ее можно записать как: $\psi (q_1,\ q_2)$, где для бесспиновых частиц понимают под $q_1$ совокупность трех пространственных координат одной частицы, под $q_2$ координаты второй частицы. (В том случае, если частица обладает спином, то к пространственным координатам добавляют спиновые координаты).
Если переставить местами частицы $1$ и $2$, то получают волновую функцию $\psi \left(q_2,\ q_1\right).$ Данную операцию можно представить как действие линейного оператора $\hat{P}$ на функцию $\psi (q_1,\ q_2)$, при этом оператор называют оператором перестановки:
Переставим исследуемые частицы второй раз, имеем:
Из выражения (2) следует, что ${\hat{P}}^2=1$, значит $\hat{P}=\pm 1.\ $Следовательно, допускаются волновые функции следующих типов:
В случае (3) волновая функция при перестановке частиц не изменяется, ее называют симметричной (имеет индекс $s$). В случае (4) мы имеем асимметричную функцию, имеет индекс $a$. Она изменяет знак при перестановке однотипных частиц.
Данные результаты обобщаются для систем имеющих любое количество одинаковых частиц. Тогда симметрия или асимметрия проявляется при перестановке любых двух частиц.
Частицы, которые описываются симметричными волновыми функциями, называют бозе-частицами (бозонами). Частицы, которые описываются антисимметричными волновыми функциями, названы ферми -- частицами (фермионами).
Принцип Паули
В системе тождественных фермионов не существует двух частиц, которые находятся в одном состоянии. Данной положение называют принципом (запретом) Паули. Данное предположение Паули выдвинул еще до возникновения квантовой механики. В следующем виде:
В атоме не может быть двух электронов, которые бы характеризовались одинаковыми четверками квантовых чисел. Принцип Паули выполняется относительно отдельных частиц, которые не взаимодействуют. Данный принцип использовался для обоснования периодической системы Менделеева, части закономерностей в спектрах.
Относительно бозонов нет подобных ограничений. В одном и том же состоянии может существовать любое количество бозонов.
Что такое детерминант Слэтера?
Решение:
Рассмотрим систему из $N$ --одинаковых микрочастиц. Волновая функция ($\psi$) такой системы должна подчинять принципу тождественности, то есть быть симметричной или асимметричной, то есть:
\[\psi\left(q_1,\dots ,q_i,{\dots ,q}_j\dots ,q_N\right)=\psi\left(q_1,\dots ,q_j,{\dots ,q}_i\dots ,q_N\right)\left(1.1\right).\]Если частицы не взаимодействуют друг с другом, антисимметричная волновая функция, которая удовлетворяет принципу тождественности, может быть представлена в виде:
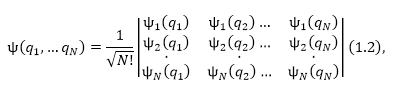
Рисунок 1.
где $\psi_i\left(q_i\right)$ -- волновые функции для одной частицы. Много частичная волновая функция, представленная в виде (1.2) называется детерминантом Слэтера. В такой записи перестановка микрочастиц местами эквивалентна перестановке пары столбцов в определителе (1.2). Как известно, при подобной перестановке определитель изменяет знак, что значит - волновая функция асимметрична относительно перестановки любой пар частиц.
Охарактеризуйте состояние, которое в квантовой механике называют перепутанным.
Решение:
Допустим, что мы имеем систему из двух не взаимодействующих электронов. Волновую функцию такой системы $\psi\left(q_1,q_2\right)$ представим в виде выражения:
\[\psi\left(q_1,q_2\right)=\psi_1\left(q_1\right)\psi_2\left(q_2\right)\left(2.1\right),\]где $\psi_1\left(q_1\right)$ -- волновая функция одной частицы, $\psi_2\left(q_2\right)$ -- волновая функция другой частицы. Выражение (2.1) принципу тождественности не удовлетворяет. Так как при перестановке частиц мы получим иное состояние:
\[\psi\left(q_2{,q}_1\right)=\psi_1\left(q_2\right)\psi_2\left(q_1\right)\left(2.2\right).\]Но, для имеющихся волновых функций $\psi_1\left(q\right){\ и\ \psi}_2\left(q\right)$ можно создать две комбинации, которые удовлетворяют свойствам симметрии. Причем одна является симметричной относительно перестановки:
\[\psi_s\left(q_1,q_2\right)=\frac{1}{\sqrt{2}}\left(\psi_1\left(q_1\right)\psi_2\left(q_2\right)+\psi_1\left(q_2\right)\psi_2\left(q_1\right)\right)\left(2.3\right),\]другая асимметричной по отношению к перестановке электронов:
\[\psi_a\left(q_1,q_2\right)=\frac{1}{\sqrt{2}}\left(\psi_1\left(q_1\right)\psi_2\left(q_2\right)-\psi_1\left(q_2\right)\psi_2\left(q_1\right)\right)\left(2.4\right).\]Существенным свойством полученных состояний является то, что даже в отсутствии взаимодействия (в общем случае) $\psi$ -- функция одинаковых частиц не представима как произведение волновых функций для отдельных частиц. Такое состояние, при котором выполняется условие:
\[\psi_{s(a)}\left(q_1,q_2\right)\ne {\varphi }_1\left(q_1\right){\varphi }_2\left(q_2\right)(2.5)\]называют перепутанным.











