Основное уравнение квантовой механики было предложено Э. Шредингером в $1926$ г. Его значение в квантовой физике аналогично значению уравнению движения И. Ньютона. Уравнение Шредингера не выводится, оно постулируется. Его истинность доказывается тем, что полученные с его помощью результаты хорошо согласуются с экспериментами, проводимыми в рамках атомной и ядерной физики. Уравнение Шредингера можно представить в следующем виде:
\[-\frac{\hbar }{i}\frac{\partial \Psi}{\partial t}=-\frac{{\hbar }^2}{2m}\triangle \Psi+U\left(x,y,z,t\right)\Psi\left(1\right),\]где $\hbar =\frac{h}{2}=1,05\cdot {10}^{-34}Дж\cdot с\ $- постоянная Планка, $m$ -- масса частицы, $U\left(x,y,z,t\right)$- потенциальная энергия частицы в силовом поле в котором перемещается частица, $\triangle =\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}$ -- оператор Лапласа, $\Psi=\Psi(x,y,z,t)$ -- волновая функция частицы, $i=\sqrt{-1}$ -- мнимая единица.
Уравнение (1) является справедливым для любой частицы, которая движется со скоростью много меньшей скорости света ($v\ll c,\ где\ c\ $-- скорость света в вакууме). Уравнение Шредингера дополняют условиями, которые накладываются на волновую функцию $\Psi\ (x,y,z,t)$:
-
Данная функция должна быть конечной, непрерывной и однозначной.
-
Производные от этой функции ($\frac{\partial \Psi}{\partial x},\ \frac{\partial \Psi}{\partial y},\frac{\partial \Psi}{\partial z},\frac{\partial \Psi}{\partial t}$) должны быть непрерывны.
-
Функция ${\left|\Psi\right|}^2$ должна быть интегрируемой, что означает, интеграл $\iiint\limits^{\infty }_{-\infty }{{\left|\Psi\right|}^2dxdydz}$ должен быть конечным. В самом простом случае данное условие сводится к условию нормировки вероятностей. Это условие связано с тем, что физическим смыслом обладает не сама волновая функция, а ${\left|\Psi\right|}^2$.
Значение вышеперечисленных условий в том, что с их помощью не решая уравнения Шредингера, только изучая возможные решения, можно делать ряд важных выводов об энергии и других параметрах рассматриваемой частицы.
Уравнение (1) называют временн$\acute{ы}$м уравнением Шредингера, так как оно содержит производную от волновой функции по времени.
Стационарное уравнение Шредингера
Для большого числа явлений, которые происходят в микромире можно использовать стационарную волновую функцию (независящую от времени) и соответственно стационарное уравнение Шредингера. Такое уравнение имеет смысл для задач, в которых потенциальная энергия не зависит от времени ($U=U\left(x,y,z\right)$).
Решение уравнения (1) найдем в виде:
Подставим выражение (2) в уравнение Шредингера (1), получим:
Разделим обе части выражения (3) на произведение функций $\varphi \Psi$, имеем:
В уравнении (4) левая часть -- функция только координат, правая -- только времени. Равенство возможно только в случае, если обе части уравнения равны некоторой постоянной. Обозначим ее $-E$ и запишем:
Уравнение (6) называют стационарным уравнением Шредингера. Оно является важным уравнением в квантовой механике и играет основную роль в атомной физике. Функции $\Psi$, которые удовлетворяют уравнению Шредингера при известной U, называют собственными функциями. Величины $E$ при которых существуют решения уравнения Шредингера (6) называют собственными значениями.
Уравнение (5) можно проинтегрировать. Получим:
где ${\varphi }_0=\varphi_0\left(0\right)$- значение $\varphi (t)$ в начальный момент времени (t=0).
Для определения смысла величины $E$ в стационарном уравнении Шредингера уравнение (6) сравнивают с волновым уравнением:
где $v^2_{faz}$ -- фазовая скорость волн в квадрате. Для синусоидальных волн ($S=A\left(r\right)e^{-i2\pi \nu (t-\frac{r}{v_{faz}})},\ \ где\ \nu \ --\ частота\ волны$):
уравнение (8) записывается как:
К волнам де Бройля, которые связаны с движущимися частицами, можно применять уравнение (9). Для длины волны де Бройля известно соотношение:
где $v_{faz}$- фазовая скорость волн де Бройля, $\nu $ -- частота волн де Бройля. Подставим вместо $\frac{\nu }{v_{faz}}$ в уравнение (10) в соответствии с (11) величину $\frac{mv}{h}$, вместо $S$ волновую функцию, получим:
$\frac{mv^2}{2}=E-U$ -- кинетическая энергия частицы, где $E$ -- ее полная энергия. Выражение $\frac{4{\pi }^2m^2v^2}{h^2}$ перепишем как:
Значит в уравнении (12) имеем:
Мы получили уравнение (14) тождественное со стационарным уравнением Шредингера. Рассуждения, приведенные выше, подчеркивают волновой характер уравнения Шредингера. Надо отметить, что представление полной энергии ($E$) как суммы потенциальной и кинетической энергии в квантовой механике имеет ограниченный характер.
Уравнение Шредингера находится в согласии с предположением о связи полной энергии ($E$) частицы с частотой волн де Бройля. Решение уравнения Шредингера можно записать в виде:
Так, состояние частицы в рассматриваемый момент времени можно описать периодической функцией времени, имеющей циклическую частоту ($\omega =\frac{E}{\hbar }$), которая определена полной энергией частицы.
Задание: На пути электронного пучка, имеющего энергию $E$, расположен потенциальный барьер высоты $U$ ($U >E$) (рис.1). Какова относительная вероятность пребывания электрона в области $2$ на расстоянии x от границы областей $1$ и $2$ ($\epsilon$)?
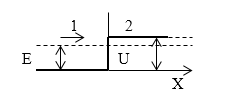
Рисунок 1.
Решение:
В задаче следует найти отношение плотности вероятности нахождения электрона в точке $x$ к плотности вероятности его нахождения на границе областей. В задаче имеется высокий потенциальный барьер бесконечной ширины. Все падающие на барьер электроны отражаются от него, но существует вероятность, что электрон попадет в область $2$. Для нахождения вероятности обнаружения электрона в области $2$ надо решить уравнение Шредингера вида:
\[\triangle \Psi+\frac{2m}{{\hbar }^2}\left(E-U\right)\Psi=0\left(1.1\right).\]Для одномерного случая, который мы имеем для нашей задачи уравнение (1.1) примет вид:
\[\frac{{\partial }^2\Psi}{\partial x^2}-\frac{2m}{{\hbar }^2}\left(E-U\right)\Psi=0\left(1.2\right).\]Решение данного уравнения функция:
\[\Psi\left(x\right)=Ce^{kx}+De^{-kx}\left(1.3\right),\]где $C$ и $D$ постоянные. Однако, из (1.3) при $x\to \infty ,$ то$\ \Psi\to \infty $, что не допустимо, следовательно, $C=0$. Получаем:
\[\Psi\left(x\right)=De^{-kx}=De^{-\frac{\sqrt{2m(U-E)x}}{\hbar }}\left(1.4\right).\]Используя (1.4) найдем плотность вероятности нахождения частицы в точке x как:
\[{p=\left|\Psi(x)\right|}^2=D^2e^{-\frac{2\sqrt{2m\left(U-E\right)x}}{\hbar }}\left(1.5\right).\]Плотность вероятности, исходя из (1.5) на границе ${p_0=\left|\Psi (0)\right|}^2=D^2$. Тогда относительная вероятность ($\epsilon$) равна:
\[\epsilon=\frac{{\left|\Psi(x)\right|}^2}{{\left|\Psi(0)\right|}^2}=e^{-\frac{2\sqrt{2m\left(U-E\right)x}}{\hbar }}.\]Ответ: $\epsilon=e^{-\frac{2\sqrt{2m\left(U-E\right)x}}{\hbar }}.$
Задание: Запишите уравнение Шредингера для электрона в водородоподобном атоме.
Решение:
Для написания необходимого уравнения следует вспомнить формулу, определяющую потенциальную энергию, которой обладает электрон в водородоподобном атоме, находящийся на орбите радиуса r:
\[U=-\frac{Zq^2_e}{4\pi {\varepsilon }_0r}\left(2.1\right).\]Уравнение для электрона в водородоподобном атоме должно быть стационарным и его можно записать как:
\[\triangle \Psi+\frac{2m_e}{{\hbar }^2}\left(E+\frac{Zq^2_e}{4\pi {\varepsilon }_0r}\right)=0.\]Ответ: $\triangle \Psi+\frac{2m_e}{{\hbar }^2}\left(E+\frac{Zq^2_e}{4\pi {\varepsilon }_0r}\right)=0.$











