Распределение плотности электронного облака в атоме водорода
Рассмотрим пространственную структуру атома водорода в стационарном состоянии.
Вероятность нахождения электрона в элементе объема:
возле точки с координатами $r,\theta ,\varphi $ равна:
где квантовые числа опустим для сокращения записи, $R(r)$ -- радиальная функция, $Y\left(\theta ,\varphi \right)-угловая\ фунекиция$. Вероятности (2) ставят в соответствие представление об электроне в виде облака, которое имеет плотность. Причем эта плотность пропорциональна ${\left|\psi(r,\theta ,\varphi )\right|}^2$. Величина $q_e{\left|\psi(r,\theta ,\varphi )\right|}^2=\rho $ называется плотностью заряда электрона и считается непрерывно распространенной в пространстве. Часто используют следующую интерпретацию: Полагают, что электрон обегает пространство, которое занимает атом, при этом время пребывания электрона в объеме dV пропорционально${\left|\psi(r,\theta ,\varphi )\right|}^2.$
Структура электронного облака задает пространственную конфигурацию атома. Часто, для упрощения, рассматривают радиальное и угловое распределения плотности облака отдельно.
Вероятность обнаружить электрон в шаровом слое $r\ и\ r+dr\ $ равна:
Плотность вероятности для координаты r при этом описано функцией:
Используя радиальные волновые функции ($R_{nl}$) в явном виде для состояний атома водорода можно из выражения (4) найти зависимости плотности электронного облака от расстояния $(r)$. Отметим, что вероятность обнаружения электрона очень близко к ядру и на больших расстояниях от ядра мала. Плотность облака существенна на конечных расстояниях от ядра.
Нахождение средних расстояний дает формулу:
где $r_B$ -- Боровский радиус.
Из формулы (5) видно, что $\left\langle r_{nl}\right\rangle $ растер при увеличении $n$ (главного квантового числа), при установленном $n$ уменьшается в зависимости от роста орбитального квантового числа ($l$).
Четкой границы у атома не существует, но плотность электронного облака по экспоненте уменьшается при $r >\left\langle r\right\rangle $. В состоянии $l=n-1$ имеем:
Рассмотрим угловое распределение электронного облака. Вероятность нахождения электрона в пределах элемента телесного угла ($d\Omega =sin\theta d\theta d\varphi $) в направлении, которое задается углами $\theta $ и $\varphi $ равна:
При этом плотность вероятности равна:
Функция $Y_{lm}\sim e^{im\varphi }$, следовательно $p_{lm}$ от угла $\varphi $ не зависит. Следовательно, электронное облако имеет осевую симметрию.
Распределение по полярному углу $\theta $ обычно представляют графически в полярных диаграммах. При этом на полярной оси от начала координат откладывают величины $p_{lm}$. Через полученные точки проводят линию. Чем дальше точки от начала координат, тем выше вероятность найти частицу в исследуемом направлении.
Для больших величин $n\ и\ l$ строение атома водорода весьма сложное.
Плотность электронного облака в атоме со многими электронами
Пусть пара сопряженных величин: координата $q$ и импульс $p$ определяют координаты точки в $pq$ - плоскости. Перейдя к движению в пространстве, имеем три координаты и три импульса ($6$-мерное пространство). Положим, что все электроны в атоме имеют одинаковые условия. Каждый электрон подчинен закону сохранения энергии (его потенциальная энергия равна $q_e\varphi ,\ \varphi $ -- средний потенциал). В каждой ячейке объемом $h^3$ может находиться только два электрона, при этом максимальный их имеющихся импульсов равен $p_{max}$. Плотность электронов можно выразить как ($p \[\rho =-\frac{8\pi q_e}{3}{\left(\frac{p_{max}}{h}\right)}^3\left(9\right).\]
Электростатический потенциал в атоме
Если известны, плотность заряда ($\rho $) и импульс ($p_{max}$), то их можно связать с электростатическим потенциалом (${\varphi }_e$). Для этого используется уравнение Пуассона, считая, что $\rho $ и ${\varphi }_e$ симметричны относительно ядра и зависят только от расстояния до него. Данное уравнение принимает вид:
Из закона сохранения энергии имеем:
Принимая во внимание то, что в атоме связаны только те электроны, для которых работа, требуемая для переноса их на поверхность атома, положительна. Рассматривая ионы с зарядом равным $Zq_e,$ вводим сферу радиуса $R$, вне которой потенциал имеет кулоновский вид:
Этот потенциал учитывается при подсчете работы, которая необходима для удаления электрона. Будем считать, что $E=0$ для электрона на этой сфере, получаем для максимального импульса выражение:
На потенциал накладываются граничные условия вида:
Так как около ядра вклад электронов в потенциал несущественный, то следующее граничное условие запишем как:
Подставим выражение (11) в формулу (9) получаем:
Если умножить выражение (14) на $\frac{1}{{\varepsilon }_0}$, то получим правую часть уравнения Пуассона. То есть (10) примет вид:
Уравнение Пуассона содержит одну неизвестную функцию.
Задание: На каком расстоянии от ядра $(r)$ в состоянии с орбитальным квантовым числом $l=n-1$ плотность вероятности обнаружить электрон максимальна? Рассмотреть атом водорода в стационарном состоянии.
Решение:
В состояниях с $l=n-1$ функция плотности вероятности для атома водорода в стационарном состоянии имеет вид:
\[p\left(r\right)\sim r^{2n}{\exp \left(-\frac{2r}{nr_B}\right)\ \left(1.1\right).\ }\]Для нахождения экстремума функции возьмем производную от $p\left(r\right)$ по $r$ приравняем ее к нулю:
\[\frac{dp}{dr}=\left[2nr^{2n-1}{exp \left(-\frac{2r}{nr_B}\right)-\ r^{2n}\ }\frac{2}{nr_B}{exp \left(-\frac{2r}{nr_B}\right)\ \ }\right]=2{exp \left(-\frac{2r}{nr_B}\right)r^{2n}\ \ }\left[\frac{n}{r}-\frac{1}{nr_B}\right]=0\left(1.2\right).\] \[\frac{n}{r}-\frac{1}{nr_B}{\rm =0}\to {\rm r=}n^2r_B.\]Ответ: Максимума функция $p\left(r\right)$ достигает в точке ${\rm r}{\rm =}n^2r_B.$ Расстояния совпадают с радиусами круговых орбит.
Задание: Рассмотрите состояния атома водорода, которые описываются угловыми функциями: $Y_{00}=\frac{1}{\sqrt{4\pi }},\ Y_{10}=\sqrt{\frac{3}{4\pi }}cos\theta $. Изобразите полярные диаграммы. Чему равна вероятность нахождения электрона на полярной оси?
Решение:
Рассмотрим функцию $Y_{00}=\frac{1}{\sqrt{4\pi }}$. Из формулы видим, что $l=0,\ m=0.$ В s -- состоянии облако имеет сферическую симметрию (рис.1).
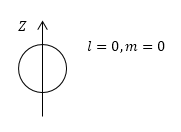
Рисунок 1.
Для функции $Y_{10}=\sqrt{\frac{3}{4\pi }}cos\theta $ имеем $l=1,\ m=0.$ В $p$ -- состоянии при $m=0$ электронное облако вытянуто по оси $Z$ (рис.2).

Рисунок 2.
Ответ: На полярной оси вероятность обнаружить электрон равна нулю.














