Одноэлектронный атом
Одноэлектронный атом -- это простейшая система, рассматриваемая в квантовой механике, которая состоит из электрона, движущегося в кулоновском поле положительно заряженного ядра (заряд ядра равен $Z\left|q_e\right|$). Данную систему еще называют водородоподобной. При $Z=1$ мы получаем атом водорода, $Z=2$ имеем ион атома гелия (${He}^+$), при $Z=3$ -- дважды ионизированный атом лития (${Li}^{++}$) и далее. Потенциальная энергия взаимодействия электрона с ядром в данной системе, будет равна:
где $r$ -- расстояние от электрона до ядра. В первом приближении ядро считают точечным.
Уравнение Шредингера с центрально - симметричным потенциалом
В атомной физике более важным является случай, когда потенциальная функция $(U)$ не является одномерной, а является сферически симметричной по отношению к некоторому силовому центру (например, ядру). Начало координат разместим в силовом центре, который считаем неподвижным. Через $\overrightarrow{{\rm r}}$, обозначим радиус-вектор, который проведен из силового центра к рассматриваемой частице. Тогда в данном случае $\psi$ -- функция зависит от ${\rm r\ и\ }$угловых переменных, которые определяют направление вектора $\overrightarrow{{\rm r}}$.
Уравнение Шредингера для водородоподобных атомов, исходя из выражения для потенциальной энергии (2) можно записать как:
Из выражения для потенциальной энергии (1) видно, что поле, в котором совершает движение электрон, обладает центральной симметрией, то есть зависит только от расстояния ($r$). Решение уравнения (2), обычно выполняют в сферических координатах ($r,\theta ,\varphi $), где оператор Лапласа имеет вид:
Оператор Гамильтона для электрона в кулоновском поле статичного ядра в сферической системе координат принимает вид:
где $m$ -- масса электрона, ${\hat{L}}^2$ -- оператор квадрата момента импульса.
Решение уравнения (2) проводят методом разделения переменных, учитывая естественные требования, накладываемые на волновую функцию. Данные требования удовлетворяются при любых положительных значениях энергии $E$, однако, в области отрицательных значений $E$ только при дискретных, если:
Связанным состояниям электрона (электрон в атоме) соответствует $E0$ движение электрона называют свободным, при этом энергия принимает непрерывные значения (спектр непрерывен), что соответствует ионизированному атому. Энергия ионизации водорода равна: $E_i=-E_1=13,55\ эВ$.
При решении задачи о спектре водородоподобного атома для объяснения спектральных серий схему энергетических уровней дополняют правилами отбора при излучении фотонов. Переходы между энергетическими уровнями, которые соответствуют сферически симметричным состоянием атома, являются запрещенными (не сопровождаются дипольным излучением).
Стационарное уравнение Шредингера в операторном виде (используя оператор Гамильтона) для собственных волновых функций и величин энергии E электрона имеет вид:
Так как оператор Гамильтона коммутирует с оператором ${\hat{L}}^2$, следовательно, они имеют общие собственные функции. Собственные функции уравнения (4) (\psi- функции) включают три параметра (целых числа): $n,l,m$, которые называют квантовыми числами:
где $m$- магнитное квантовое число, принимающее значения $m=0,\pm 1,\pm 2,\dots \pm l.$
$R\left(r\right)$ -- радиальная функция, $Y_{l,m}\left(\theta ,\varphi \right)$ -- сферическая функция. Радиальная функция, в свою очередь удовлетворяет уравнению:
В простейшем случае ограничиваются только сферически -- симметричными решениями (решениями, которые зависят только от $\left|\overrightarrow{r}\right|$). При этом уравнение Шредингера для стационарных состояний примет вид:
Решение уравнения Шредингера для водородоподобной системы в сферических координатах дает значимые результаты. Получается, что момент импульса электрона $(L)$ в атоме квантуется:
где $l=0,1,2\dots n-1$ --орбитальное кантовое число.
Задание: Вид волновой функции, которая описывает основное состояние электрона в атоме, водорода выражена функцией: $\psi=Ae^{-\frac{r}{a}}$, где $r$ -- расстояние от силового центра, $a$- первый Боровский радиус. Каково среднее значение $\left\langle r^2\right\rangle $ от электрона до ядра внутри атома в основном состоянии?
Решение:
Для вычисления $\left\langle r^2\right\rangle $ используем формулу:
\[\left\langle r^2\right\rangle =\int\limits^{\infty }_0{r^2}{\left|\psi(r)\right|}^2dV\ \left(1.1\right).\]Но прежде найдем коэффициент $A$, находящийся в выражении для $\psi$ -- функции их условия нормировки:
\[\int\limits_V{{\left|\psi(r)\right|}^2dV\ }=1\ \left(1.2\right),\]где $dV=4\pi r^2dr.$ Для нахождения ${\left|\psi(r)\right|}^2$ используем выражение для волновой функции из условия задачи:
\[{\left|\psi(r)\right|}^2=A^2e^{-2\frac{r}{a}}\left(1.3\right).\]Подставим выражение (1.3) в условие нормировки, учтем формулу для объема шарового слоя ($dV$), получим:
\[\int\limits^{\infty }_0{A^2e^{-2\frac{r}{a}}4\pi r^2dr\ }=A^24\pi \int\limits^{\infty }_0{e^{-2\frac{r}{a}}r^2dr\ }=A^24\pi \frac{2!}{{\left(\frac{2}{a}\right)}^3}=A^2\pi a^3=1\ \left(1.4\right).\]Из выражения (1.4) получаем:
\[A=\frac{1}{\sqrt{\pi a^3}}\left(1.5\right).\]Применяя выражение (1.5) запишем волновую функцию как:
\[\psi=\frac{1}{\sqrt{\pi a^3}}e^{-\frac{r}{a}}\left(1.6\right).\]Подставим $\psi$ -- функцию из (1.6) в формулу (1.1), имеем:
\[\left\langle r^2\right\rangle =\int\limits_V{r^2}\frac{1}{\pi a^3}e^{-2\frac{r}{a}}dV=\int\limits^{\infty }_0{r^2}\frac{1}{\pi a^3}e^{-2\frac{r}{a}}4\pi r^2dr=\ \frac{4}{a^3}\int\limits^{\infty }_0{r^4}e^{-2\frac{r}{a}}dr=\frac{4}{a^3}\frac{4!}{{\left(\frac{2}{a}\right)}^5}=3a^2\left(1.7\right).\]Ответ: $\left\langle r^2\right\rangle =3a^2$.
Задание: Изобразите график потенциальной энергии взаимодействия электрона с ядром в атоме водорода, отметьте возможные дискретные значения энергии на нем.
Решение:
Уравнение Шредингера для стационарных состояний электрона в атоме водорода имеет вид:
\[\triangle \psi+\frac{2m}{{\hbar }^2}\left(E-U\right)\psi=0\left(2.1\right),\]где $U=-\frac{q^2_e}{4\pi {\varepsilon }_0r}.$ При этом собственные значения энергии, удовлетворяющие уравнению (2.1):
\[E_n=-\frac{m{q_e}^4}{32{{{\pi }^2\varepsilon }_0}^2{\hbar }^2}\frac{1}{n^2}\ \left(n=1,2,3\dots \right)\left(2.2\right).\]Тогда: $E_1=-\frac{m{q_e}^4}{32{{{\pi }^2\varepsilon }_0}^2{\hbar }^2},$ $E_2=-\frac{m{q_e}^4}{32{{{\pi }^2\varepsilon }_0}^2{\hbar }^2}\frac{1}{4},\ E_3=-\frac{m{q_e}^4}{32{{{\pi }^2\varepsilon }_0}^2{\hbar }^2}\frac{1}{9}\dots .$ Используя выражение для $U$, изобразим функцию $U(r)$ на рис.1. Отметим соответствующие $E_n$.
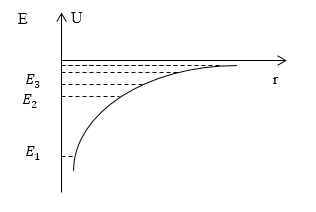
Рисунок 1.












