В химии волновую функцию электрона, которая зависит от квантовых чисел ($n,l,m$) называют орбиталью. Любая орбиталь может иметь два электрона, проекции спинов которых равны:
Когда вступают во взаимодействие два атома, происходит перекрытие их орбиталей. Как результат: повышается электронная плотность вероятности между ними. Это значит, что имеется связывающая молекулярная орбиталь. Или происходит понижение концентрации, то есть происходит разрыхление молекулярной орбитали.
Молекула водорода
Рассмотрим молекулу водорода. 1s орбитали двух атомов водорода могут сочетаться, при этом возникает связывающая орбиталь ($\Psi_S$) или разрыхляющая орбиталь $(\Psi_A)$. В терминах физики $\Psi_S$ записывается как $1s{\sigma }_g$ орбиталь, а $\Psi_A$ как $1s{{\sigma }_u}^*$ - орбиталь. Символ 1s указывает атомные орбитали, которые «смешиваются», создавая молекулярную орбиталь. Греческая буква $\sigma $ показывает то, что молекулярное состояние не имеет количества движения по отношению к оси связи. Данная составляющая момента количества движения молекулы квантована ее возможные значения:
Молекулярные состояния при $\lambda =0$ обозначают буквой $\sigma $, $при\ \ \lambda =1$ молекулярное состояние обозначают буквой $\pi $, при $\lambda =2$ буквой $\delta $, дальше по алфавиту.
Симметричные орбитали отмечают буквой $g$ (gerade (нем) - четный), антисимметричные орбитали - буквой -$u$ (ungerade (нем) - нечетный). При этом понятие симметричная значит, что орбиталь не изменяет знака, когда проходит среднюю точку между ядрами. Антисимметричная орбиталь изменяет знак при инверсии координат. Различия, которые отражают индексы g и u являются существенными только для гомоядерных двухатомных молекул ($H_2,\ O_2,\ N_2$). Разрыхляющая орбиталь обозначается звездочкой.
Рис. 1 представляет схему ограничивающих поверхностей, которые показывают создание молекулярных орбиталей $\sigma \ $ из атомных орбиталей s в гомоядерных молекулах, состоящих их двух атомов. При этом $\sigma $ -- орбитали имеют вращательную симметрию относительно оси связи. Ось $Z$ проходит вдоль межъядерной оси молекулы.
Для того чтобы определять порядок заселения орбиталей, следует знать относительные энергии разных молекулярных орбиталей. Для нахождения расположения молекулярных энергетических уровней рассматривают предельные значения межъядерных расстояний ($R$) в молекуле: в случае объединенного атома, когда $R=0$, и если атомы раздельные, то $R=\infty $.
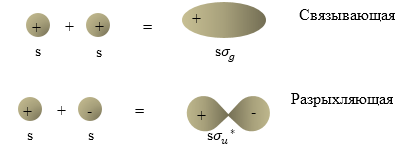
Рисунок 1. Молекулярная орбиталь. Автор24 — интернет-биржа студенческих работ
После этого изображают последовательность энергоуровней объединенного атома с одной стороны корреляционной диаграммы, и ряд уровней энергии отдельных атомов в другой части диаграммы. При помощи линий соединяют состояния с одинаковыми величинами $\lambda $, тогда появляется последовательность молекулярных энергоуровней в виде функции от $R$. Для гомоядерных молекул при этом сохраняется симметричный или антисимметричный характер орбиталей. Это получается как результат соединения орбиталей, обладающих одинаковым характером для раздельных и объединенного атомов.
В молекулярно - орбитальном подходе надо учитывать то, что заполненная связь между двумя атомами требует двух электронов. Считают, что электроны в связывающей и разрыхляющей орбиталях почти одинаково влияют на стабильность молекул. Надо отметить, что влияние связывающей и разрыхляющей орбиталей в молекуле является противоположным. При этом каждая занятая разрыхляющая орбиталь в молекуле компенсирует одну занятую связывающую орбиталь. Количество связей в молекуле определено формулой: количество связей равно $\frac{1}{2}$ (число электронов в связывающих орбиталях минус количество электронов на разрыхляющих орбиталях). Так, например, в $H_2$ имеется одна связь, а в ${He}_2$ нет связей.
При этом метод представления волновой функции молекулы как суммы или разности атомных орбиталей называют методом линейных комбинаций атомных орбиталей (методом орбиталей). В таком методе истинные молекулярные орбитали, заменяют линейными комбинациями атомных орбиталей.
Ион молекулы водорода
Рассмотрим ион молекулы водорода ($H^+_2$). Атомные орбитали, при помощи которых строят волновую функцию этого иона - волновые функции основных состояний $\Psi_a\ и\\Psi_b$, которые относятся к атомам водорода в точках $a$ и $b$. Допустим, что орбитали $\Psi_a\ и\ \Psi_b$нормированы на единицу, тогда волновые функции молекул, построенные по методу орбиталей, примут вид:
где $\Psi_c$- симметричная волновая функция и $\Psi_{ac}$ -- антисимметричная волновая функция. $A_c\ и\ A_{ac}$ -- нормировочные множители (постоянные). Функции $\Psi_c$ и $\Psi_{ac}$ должны быть нормированы на единицу. Следовательно:
Если ввести обозначение:
то выражение (4) примет вид:
Аналогично можно получить:
Интеграл (5) называется интегралом перекрытия. Он показывает количественную меру перекрытия волновых функций $\Psi_a\ и\ \Psi_b$. Для иона молекулы водорода интеграл перекрытия равен:
где $r_b-\ $радиус боровской орбиты атома водорода. В ионе молекулы водорода равновесному состоянию отвечает $R=2r_b$, $q=0,6.$
Задание: Запишите выражение для энергии электрона в ионе молекулы водорода, используя волновые функции основных состояний атомов водорода.
Решение:
Если обозначить волновые функции основных состояний $\Psi_a\ и\Psi_b$, которые относятся к атомам водорода в точках $a$ и $b$, то энергию электрона в симметричном состоянии можно записать как:
\[E_c=\int{{\Psi_c}^*\hat{H}}\Psi_cdV\ \left(1.1\right),\]где $\hat{H}=-\frac{\hbar }{2m}{\nabla }^2-\frac{q^2_e}{4\pi {\varepsilon }_0}(\frac{1}{r_a}+\frac{1}{r_b})$ -- оператор Гамильтона для электрона.
В антисимметричном состоянии имеем:
\[E_{ac}=\int{{\Psi_{ac}}^*\hat{H}}\Psi_{ac}dV\ \left(1.2\right).\]Задание: Изобразите схему ограничивающих поверхностей, которая иллюстрирует образование молекулярных $\sigma -\ $орбиталей из атомных орбиталей $p_z$ в гомоядерной двухатомной молекуле (рис.2).
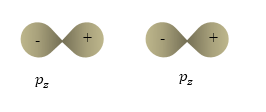
Рисунок 2. Молекулярная орбиталь. Автор24 — интернет-биржа студенческих работ
Решение:
Считаем, что ось $Z$ проходит по межъядерной оси молекулы.
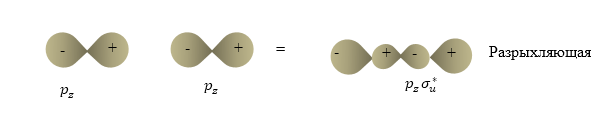
Рисунок 3. Молекулярная орбиталь. Автор24 — интернет-биржа студенческих работ
При схождении двух атомов в указанной на рис.2 ситуации возникает разрыхляющая молекулярная орбиталь (рис.3).











