Молекула
Молекулой называют самую маленькую частицу однородного вещества, которая имеет его основные химические свойства. Молекулы могут состоять из одинаковых или разных атомов, которые соединяются между собой химическими связями.
Молекулы являются устойчивыми структурами. Их устойчивость говорит о том, что химические связи вызываются силами взаимодействия, которые связывают атомы в молекулы. Эмпирически доказано, что для разъединения молекул на составные части (атомы) следует выполнить работу.
Значит, процесс образования молекулы должен быть сопровожден выделением энергии. Так, 2 атома водорода, пребывающие в свободном состоянии имеют большую энергию, чем те же атомы в двухатомной молекуле $H_2.$ Энергия, выделяемая при образовании молекулы, служит мерой работы сил взаимодействия, которые связывают атомы в молекулу.
Создание молекулы -- это исключительно квантовый эффект, который не объясним в классической физике. При помощи квантовой механики можно получить волновые функции молекулы и вычислить энергоуровни, определить расстояние между ядрами атомов, при которых энергия минимальна, определить заряды атомов, дипольный момент и порядки связей. Однако следует отметить, что и квантовая механика пока не может объяснить соединение атомов в молекулу. Причины устойчивости и не устойчивости молекул, их спектры, свойства химических связей.
Адиабатическое приближение
Если применять адиабатическое приближение для исследования структуры молекулы, то, прежде всего, следует решить задачу на собственные значения и собственные функции электронной подсистемы молекулы. При этом должна быть получена совокупность собственных функций и собственных значений, которые параметрически связаны с расстояниями между ядрами атомов в молекуле. Обычно, далее строится система термов молекулы и анализируется задача о пространственном строении молекулы и специфике движения ядер для каждого терма.
Рассмотрим молекулу, составленную из двух атомов. Простейший оператор Гамильтона для такой системы имеет вид (для краткости записи используем систему СГС):
где ${\hat{H}}_e={\hat{E}}_{ke}+U_e$- электронная компонента оператора Гамильтона, ${\hat{E}}_{ke}$ -- кинетическая энергия электрона, $U_e=-\frac{q^2_e}{r_1}-\frac{q^2_e}{r_2}$ -- энергия взаимодействия электрона с протонами, $r_1$ -- расстояние от электрона до первого протона, $r_2$ -- расстояние от электрона до второго протона, ${\hat{E}}_{k1}\ и\ {\hat{E}}_{k2}$ -- кинетические энергии ядер, $R=\left|{\overrightarrow{R}}_1-{\overrightarrow{R}}_2\right|$- расстояние между ядрами. Стационарные состояния системы можно получить, решая уравнение Шредингера:
Обычно, далее переходят в систему координат, которая связывается с центром масс молекулы. В сравнении с массой ядра ($m_{ya}$) пренебрегают массой электрона $m_e$, при этом считают, что массы ядер атомов, которые составляют молекулу одинаковы. Вводят координату центра масс:
и координату относительного движения:
В таком случае координаты ядер можно определить как:
Выражение для кинетической энергии ядер в избранной системе координат (связанной с центром масс) примет вид:
где $\mu =\frac{m_{ya}}{2}$ -- приведенная масса молекулы. Оператор Гамильтона запишем как:
где $\overrightarrow{r}$ -- координата электрона, которая отсчитывается от центра масс молекулы, учитывая, что:
Выражение (7) означает то, что гамильтониан можно представить как сумму операторов Гамильтона для двух подсистем: одна для совокупности координат, которые описывают движение электронов и ядер в молекуле, вторая для координаты центра масс $\overrightarrow{{\mathcal R}}$. Следовательно, волновая функция молекулы $\Phi \left(\overrightarrow{r},\overrightarrow{R},\overrightarrow{{\mathcal R}}\right)$ представима как:
где $e^{i\overrightarrow{K}\overrightarrow{{\mathcal R}}}$- определяет волновую функцию свободного перемещения в пространстве молекулы как единого целого, $\overrightarrow{K}$ -- волновой вектор молекулы. Функция $\Psi\left(\overrightarrow{r},\overrightarrow{R}\right)-\ $собственная функция оператора Гамильтона:
она содержит всю информацию о внутренней структуре молекулы.
Задачу на собственные функции и собственные значения для оператора Гамильтона вида (10) часто проводят в адиабатическом приближении (приближение Борна - Оппенгеймера). Суть которого, заключается в том, что считают молекулу совокупностью двух подсистем: легкой -- электронной и тяжелой - ядерной. Электроны движутся со скоростями много больше, чем скорость движения ядер. В адиабатическом приближении считают, что ядра являются неподвижными. Кроме того, полагают, что когда рассматривают ядерную подсистему, то электронная подсистема подстраивается под мгновенное расположение ядер.
В рамках рассматриваемого приближения волновую функцию $\Psi\left(\overrightarrow{r},\overrightarrow{R}\right)$ представляют как:
где $\psi^e\left(\overrightarrow{r},\overrightarrow{R}\right)$ -- электронная волновая функция молекулы (зависит от ядерной координаты как параметра), $\phi^N\left(\overrightarrow{R}\right)$ -- волновая функция ядерной подсистемы молекулы. Функция $\psi^e\left(\overrightarrow{r},\overrightarrow{R}\right)$ -- решение задачи на собственные значения уравнения вида:
где $E^e\left(R\right)$ -- энергия подсистемы электронов для молекулы. Она зависит от ядерной координаты как параметра. Решением (12) служит полная совокупность состояний электронов молекулы.
Оператором кинетической энергии ядерной подсистемы в нашем случае является:
Значимым является то, что слагаемые, которые имеют дифференцирование электронной волновой функции по ядерной координате, малы по сравнению с другими слагаемыми, которые входят в уравнение:
Данное выше утверждение -- основа адиабатического приближения с математической точки зрения. Отбросим неадиабатические члены уравнения (14) и разделим обе части его на $\psi^e\left(\overrightarrow{r},\overrightarrow{R}\right)\phi^N\left(\overrightarrow{R}\right)$, получим:
Значит, уравнение для нахождения волновых функций стационарных состояний ядерной подсистемы можно записать как:
Выражение (16) - уравнение Шредингера с эффективным потенциалом взаимодействия ядер в молекуле:
Задание: Что учитывает эффективный потенциал взаимодействия ядер в молекуле?
Решение:
Из выражения, которое определяет эффективный потенциал взаимодействия ядер в молекуле:
\[U^{eff}\left(R\right)=\frac{q^2_e}{R}+E^e\left(R\right)\left(1.1\right)\]следует, что он учитывает кулоновское отталкивание, которое существует между ядрами, как одноименно заряженными частицами, но и наличие электронной плотности в системе, которая осуществляет притяжение и может вести к связыванию атомов в молекулы. Для этого надо, чтобы зависимость $U^{eff}\left(R\right)$ была кривой, которая имеет локальный минимум. Зависимость $U^{eff}$ от расстояния между ядрами в молекуле носит название электронного терма молекулы или потенциальной поверхности (потенциальной кривой).
Задание: Потенциальная кривая взаимодействия ядер в молекуле в зависимости от межъядерного расстояния представлена на рис.1. Возможен ли такой случай?
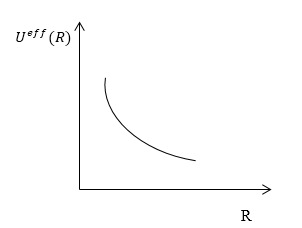
Рисунок 1. Молекула. Адиабатическое приближение. Автор24 — интернет-биржа студенческих работ
Решение:
Случай, когда потенциальная кривая не имеет минимума энергии, возможен. Тогда для любого расстояния между атомами есть силы отталкивания, и устойчивая связь атомов невозможна. Терм такой молекулы называют разлётным.











