Закон сохранения энергии - всеобщий закон природы. Следовательно, он применим в том числе, и к электрическим явлениям. Рассмотрим два случая превращения энергии в электрическом поле:
- Проводники являются изолированными ($q=const$).
- Проводники соединены с источниками тока при этом не изменяются их потенциалы ($U=const$).
Закон сохранения энергии в цепях с постоянными потенциалами
Допустим, что имеется система тел, которая может включать в себя как проводники, так и диэлектрики. Тела системы могут совершать малые квазистатические перемещения. Температура системы поддерживается постоянной ($\to \varepsilon =const$), то есть тепло подводится к системе, или отводится от нее при необходимости. Диэлектрики, входящие в систему будем считать изотропными, плотность их положим постоянной. В этом случае доля внутренней энергии тел, которая не связана с электрическим полем изменяться не будет. Рассмотрим варианты превращений энергии в подобной системе.
На любое тело, которое находится в электрическом поле, действуют пондемоторные силы (силы, действующие на заряды внутри тел). При бесконечно малом перемещении пондемоторные силы выполнят работу $\delta A.\ $Так как тела перемещаются, то изменение энергии dW. Так же при перемещении проводников изменяется их взаимная емкость, следовательно, для сохранение потенциала проводников неизменным, необходимо изменять заряд на них. Значит, каждый из источников тора совершает работу равную $\mathcal E dq=\mathcal E Idt$, где $\mathcal E $ - ЭДС источника тока, $I$ -- сила тока, $dt$ - время перемещения. В нашей системе возникнут электрические токи, и в каждой ее части выделится тепло:
По закону сохранения заряда, работа всех источников тока равна механической работе сил электрического поля плюс изменение энергии электрического поля и тепло Джоуля -- Ленца (1):
В случае если проводники и диэлектрики в системе неподвижны, то $\delta A=dW=0.$ Из (2) следует, что вся работа источников тока превращается в тепло.
Закон сохранения энергии в цепях с постоянными зарядами
В случае $q=const$ источники тока не войдут в рассматриваемую систему, тогда левая часть выражения (2) станет равна нулю. Помимо этого, тепло Джоуля - Ленца возникающее за счет перераспределения зарядов в телах при их перемещении обычно считают несущественным. В таком случае закон сохранения энергии будет иметь вид:
Формула (3) показывает, что механическая работа сил электрического поля равна уменьшению энергии электрического поля.
Применение закона сохранения энергии
Используя закон сохранения энергии в большом количестве случаев можно рассчитать механические силы, которые действуют в электрическом поле, при чем сделать это порой существенно проще, чем, если рассматривать непосредственное действие поля на отдельные части тел системы. При этом действуют по следующей схеме. Допустим необходимо найти силу $\overrightarrow{F}$, которая действует на тело в поле. Полагают, что тело перемещается (малое перемещение тела $\overrightarrow{dr}$). Работа искомой силы равна:
Далее находят все остальные изменения энергии (2) или (3), находят проекцию $F_r$ на направление $\overrightarrow{dr}$. Находят составляющие силы и саму силу.
Задание: Вычислите силу притяжения, которая действует между пластинами плоского конденсатора, который помещен в однородный изотропный жидкий диэлектрик с диэлектрической проницаемостью $\varepsilon $. Площадь пластин S. Напряжённость поля в конденсаторе E. Пластины отключены от источника. Сравните силы, которые действуют на пластины при наличии диэлектрика и в вакууме.
Решение:
Так как сила может быть только перпендикулярна пластинам, то перемещение выберем по нормали к поверхности пластин. Обозначим через dx перемещение пластин, то механическая работа будет равна:
\[\delta A=Fdx\ \left(1.1\right).\]Изменение энергии поля при этом составит:
\[dW=-\frac{\varepsilon {\varepsilon }_0E^2}{2}Sdx\ \left(1.2\right).\]Следуя уравнению:
\[\delta A+dW=0\left(1.4\right)\]получим:
\[Fdx=\frac{\varepsilon {\varepsilon }_0E^2}{2}Sdx\ \to F=\frac{\varepsilon {\varepsilon }_0E^2}{2}S\left(1.5\right).\ \]Если между пластинами находится вакуум, то сила равна:
\[F'=\frac{\varepsilon_0E^2}{2}S\left(1.6\right).\]При заполнении конденсатора, который отключен от источника, диэлектриком напряженность поля внутри диэлектрика уменьшается в $\varepsilon $ раз, следовательно, уменьшается и сила притяжения пластин во столько же раз. Уменьшение сил взаимодействия между пластинами объясняется наличием сил электрострикции в жидких и газообразных диэлектриках, которые расталкивают пластины конденсатора.
Ответ: $F=\frac{\varepsilon {\varepsilon }_0E^2}{2}S,\ F'=\frac{\varepsilon_0E^2}{2}S.$
Задание: Плоский конденсатор частично погружен в жидкий диэлектрик (рис.1). При зарядке конденсатора жидкость втягивается в конденсатор. Вычислить силу f, с которой поле действует на единицу горизонтальной поверхности жидкости. Считать, что пластины соединены с источником напряжения (U=const).
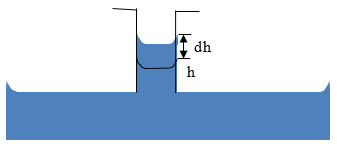
Рис. 1
Решение:
Обозначим через h- высоту столба жидкости, dh - изменение (увеличение) столба жидкости. Работа искомой силы при этом будет равна:
\[dA=Sfdh\ \left(2.1\right),\]где S -- площадь горизонтального сечения конденсатора. Изменение электрического поля равно:
\[dW=\left(\frac{\varepsilon {\varepsilon }_0E^2}{2}-\frac{{\varepsilon }_0E^2}{2}\right)Sdh\ \left(2.2\right).\]На пластины перейдет дополнительный заряд dq, равный:
\[dq=\left(\varepsilon {\varepsilon }_0E-{\varepsilon }_0E\right)adh\ \left(2.3\right),\]где $a$ -- ширина пластин, учтем, что $E=\frac{U}{d}$ тогда работа источника тока равна:
\[\mathcal E dq=Udq=U\left(\varepsilon {\varepsilon }_0E-{\varepsilon }_0E\right)adh=E\left(\varepsilon {\varepsilon }_0E-{\varepsilon }_0E\right)d\cdot a\cdot dh=\left(\varepsilon {\varepsilon }_0E^2-{\varepsilon }_0E^2\right)Sdh\left(2.4\right).\]Если считать, что сопротивление проводов мало, то $\mathcal E $=U. Используем закон сохранения энергии для систем с постоянным током при условии постоянства разности потенциалов:
\[\sum{\mathcal E Idt=\delta A+dW+\sum{RI^2dt\ \left(2.5\right).}}\]получим:
\[\left(\varepsilon {\varepsilon }_0E^2-{\varepsilon }_0E^2\right)Sdh=Sfdh+\left(\frac{\varepsilon {\varepsilon }_0E^2}{2}-\frac{{\varepsilon }_0E^2}{2}\right)Sdh\to f=\frac{\varepsilon {\varepsilon }_0E^2}{2}-\frac{{\varepsilon }_0E^2}{2}\ .\]Ответ: $f=\frac{\varepsilon {\varepsilon }_0E^2}{2}-\frac{{\varepsilon }_0E^2}{2}.$











