Сила тока
Электрический ток количественно характеризует сила тока (I), которая равна производной от заряда ($q$) по времени для тока, который течет через поверхность S:
По своей сути сила тока -- это поток заряда через поверхность S.
Электрический ток -- процесс движения, как отрицательных зарядов, так и положительных.
Перенос отрицательного заряда в одном направлении эквивалентен переносу такого же положительного заряда в противоположном направлении. В том случае, если ток создается зарядами обоих знаков $(dq^+\ и\ dq^-)$, то можно записать, что сила тока равна:
\[I=\frac{dq^+}{dt}+\frac{dq^-}{dt}\left(2\right).\]Положительным направлением тока считают направление движения положительных зарядов. Ток может быть постоянным и переменным. В том случае, если сила тока и его направление не изменяется во времени, то такой ток называют постоянным и для него выражение для силы тока можно записать в виде:
\[I=\frac{q}{\triangle t}\left(3\right),\]где сила тока определена, как заряд, который проходит через поверхность S в единицу времени. В системе СИ основной единицей измерения силы тока является Ампер (А).
\[1A=\frac{1Кл}{1с}.\]Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью
Выделим в проводнике, по которому течет ток, малый объем dV произвольной формы. Обозначим через $\left\langle v\right\rangle $-- среднюю скорость, с которой движутся носители заряда в проводнике. пусть $n_0\ $-- концентрация носителей заряда. Выберем бесконечно малую площадку dS на поверхности проводника, которая перпендикулярно скорости $\left\langle v\right\rangle $ (рис.1).
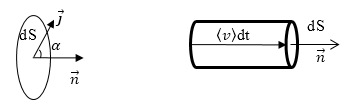
Рис. 1
Построим на площадке dS очень короткий прямой цилиндр с высотой $\left\langle v\right\rangle dt.$ Все частицы, которые находились внутри этого цилиндра за время dt пройдут через площадку dS и перенесут через нее в направлении скорости $\left\langle v\right\rangle \ $заряд равный:
\[dq=n_0q_e\left\langle v\right\rangle dSdt\left(4\right),\]где $q_e=1,6\cdot {10}^{-19}Кл$ -- заряд электрона, то есть отдельной частицы - носителя тока. Разделим выражение (4) на $dSdt$ получим:
\[j=\frac{dq}{dSdt}\left(5\right),\]где $j$ -- модуль плотности электрического тока.
\[j=n_0q_e\left\langle v\right\rangle \left(6\right),\]где $j$ -- модуль плотности электрического тока в проводнике, где заряд переносят электроны.
Если ток образуется в результате движения нескольких типов зарядов, то плотность тока можно определить как:
\[j=\sum\limits_i{n_iq_i\left\langle v_i\right\rangle \left(7\right)},\]где i -- определяет носитель заряда.
Плотность тока -- векторная величина. Обратимся вновь к рис.1. Пусть $\overrightarrow{n}$ -- единичная нормаль к площадке dS. Если частицы, которые переносят заряд положительные, то переносимый ими заряд в направлении нормали больше нуля. В общем случае элементарный заряд, который переносится в единицу времени, можно записать как:
\[\frac{dq}{dt}=\left(\overrightarrow{j}\overrightarrow{n}\right)dS=j_ndS\ \left(8\right).\]Формула (8) справедлива и в том случае, когда площадка dS неперпендикулярная вектору плотности тока. Так как составляющая вектора $\overrightarrow{j}$, перпендикулярная нормали, через площадку dS электричества не переносит. Таким образом, плотность тока в проводнике окончательно запишем, используя формулу (6) следующим образом:
\[\overrightarrow{j}=-n_0q_e\left\langle \overrightarrow{v}\right\rangle \left(9\right).\]И так, плотность тока равна количеству электричества (заряду), который протекает за одну секунду через единицу сечения проводника. Для однородного цилиндрического проводника можно записать, что:
\[j=\frac{I}{S\triangle t}\left(10\right),\]где S -- площадь сечения проводника.
Плотность постоянного тока одинакова по всему сечению проводника. Для двух разных сечений проводника ($S_1{,S}_2$) с постоянным током выполняется равенство:
\[\frac{j_1}{j_2}=\frac{S_2}{S_1}\left(11\right).\]Из закона Ома для плотности токов можно записать:
\[\overrightarrow{j}=\lambda \overrightarrow{E}\left(13\right),\]где $\lambda $ -- коэффициент удельной электропроводности.
Зная плотность тока, можно выразить силу тока как:
\[I=\int\limits_S{j_ndS\ \left(14\right),}\]где интегрирование проводят по всей поверхности S любого сечения проводника.
Единица плотности тока $\frac{A}{м^2}$.
Линии тока
Линии, вдоль которых движутся заряженные частицы, называют линиями тока.
Направлениями линий тока являются направления движения положительных зарядов. Нарисовав линии тока, получают наглядное представление о движении электронов и ионов, которые образуют ток. Если внутри проводника выделить трубку с током, у которой боковая поверхность состоит из линий тока, то движущиеся заряженные частицы не будут пересекать боковую поверхность такой трубки. Подобную трубку называют трубкой тока. Например, поверхность металлической проволоки в изоляторе будет являться трубой тока.
Задание: Сила тока в проводнике увеличивается равномерно от 0 до 5 А в течении 20 с. Найдите заряд, который прошел через поперечное сечение проводника за это время.
Решение:
За основу решения задачи примем формулу, которая определяет силу тока, а именно:
\[I=\frac{dq}{dt}\left(1.1\right).\]В таком случае заряд будет найден как:
\[q=\int\limits^{t_2}_{t_1}{Idt\ \left(1.2\right).}\]В условии задачи сказано, что сила тока изменяется равномерно, это значит, что можно записать закон изменения силы тока как:
\[I=kt\ \left(1.3\right).\]Найдем коэффициент пропорциональности в (1.3), для этого запишем закон изменения силы тока еще раз для момента времени при котором сила тока равна $I_2=$3А ($t_2$):
\[I_2=kt_2\ \to k=\frac{I_2}{t_2}\left(1.4\right).\]Подставим (1.4) в (1.3) и проинтегрируем в соответствии с (1.2), получим:
\[q=\int\limits^{t_2}_{t_1}{ktdt=\int\limits^{t_2}_{t_1}{\frac{I_2}{t_2}tdt}=\frac{I_2}{t_2}\int\limits^{t_2}_{t_1}{tdt}={\left.\frac{t^2}{2}\right|}^{t_2}_{t_1}=\frac{I_2}{{2t}_2}({t_2}^2-{t_1}^2)\left(1.5\right).}\]За начальный момент времени примем момент, когда сила тока равна нулю, то есть $t_1=0,$ $I_1=0\ А.$ $t_2=20,$ $I_1=5\ А.$
Проведем вычисления:
\[q=\frac{I_2}{{2t}_2}{t_2}^2=\frac{I_2t_2}{2}=\frac{5\cdot 20}{2}=50\ \left(Кл\right).\]Ответ: $q=50$ Кл.
Задание: Найдите среднюю скорость движения электронов в проводнике молярная масса вещества, которого равна $\mu $, поперечное сечение проводника S. Сила тока в проводнике I. Считать, что на каждый атом вещества в проводнике приходится два свободных электрона.
Решение:
Силу тока (I) в проводнике можно считать постоянной и соответственно записать, что:
\[I=\frac{q}{\triangle t}=\frac{Nq_e}{\triangle t}\left(2.1\right),\]где заряд q найдем как произведение числа электронов проводимости в проводнике, на заряд одного электрона $q_e$, который является известной величиной. $\triangle t$ -- промежуток времени за который через поперечное сечение проводника проходит заряд q.
Найти N можно, если использовать известное соотношение из молекулярной физики:
\[\frac{N'}{N_A\ }=\frac{m}{\mu }=\frac{\rho V}{\mu }\left(2.2\right),\]где $N'$- количество атомов в проводнике объем, которого V, плотность $\rho $, молярная масса $\mu $. $N_A$ -- число Авогадро. По условию задачи $N=2N'$.
Найдем из (2.2) число свободных электронов:
\[N=2\frac{\rho V}{\mu }N_A\ \left(2.3\right).\]Подставим (2.3) в (2.1), получим:
\[I=2\frac{\rho V}{\mu }N_A\frac{q_e}{\triangle t}=\frac{2\rho q_eN_ASl}{\mu \triangle t}\left(2.4\right),\]где объем проводника найден как $V=Sl$, где $l$ -- длина проводника. Выразим ее.
\[l=\frac{\mu \triangle tI}{2\rho q_eN_AS}\left(2.5\right).\]Среднюю скорость движения электронов можно найти как:
\[\left\langle v\right\rangle =\frac{l}{\triangle t}=\frac{\mu I}{2\rho q_eN_AS}.\]Ответ: $\left\langle v\right\rangle =\frac{\mu I}{2\rho q_eN_AS}.$











