Необходимые условия существования электрического тока
Упорядоченное движение заряженных частиц называют электрическим током.
Эти заряженные частицы в теории часто называют носителями тока. В проводниках и полупроводниках носителями тока являются электроны, в электролитах заряженные ионы. В газах носителями заряда могут быть и электроны и ионы. В металлах, например, могут перемещаться только электроны. Следовательно, электрический ток в них -- есть движение электронов проводимости. Надо отметить, что результат прохождения электрического тока в металлах и электропроводящих растворах существенно отличается. В металлах не происходит химических процессов при прохождении тока. Тогда как в электролитах под воздействием тока идет выделение ионов вещества на электродах (явление электролиза). Различие в результатах действия тока объясняется тем, что носители зарядов в металле и электролите принципиально различны. В металлах -- это свободные электроны, которые отделились от атомов, в растворах -- это ионы, то есть атомы или их группы, которые имею заряд.
Так, первым необходимым условием существования электрического тока, в каком -- либо веществе является наличие носителей тока.
Для того чтобы заряды находились в равновесии необходимо, чтобы разность потенциалов между любыми точками проводника была равна нулю. В том случае, если это условие нарушается, то равновесия нет, тогда заряд перемещается. Следовательно, вторым необходимым условием существования электрического тока в проводнике является создание напряжения между некоторыми точками.
Упорядоченное движение свободных зарядов, которое возникает в проводнике как результат воздействия электрического поля, называют током проводимости.
Однако отметим, что упорядоченное движение заряженных частиц возможно в том случае, если заряженный проводник или диэлектрик перемещать в пространстве. Подобный электрический ток называют конвекционным.
Механизм осуществления постоянного тока
Для того чтобы ток в проводнике шел постоянно, необходимо, чтобы к проводнику (или совокупности проводников -- цепь проводников) было присоединено какое -- либо устройство, в котором постоянно происходил процесс разделения электрических зарядов и тем самым поддерживалось напряжение в цепи. Это устройство называют источником тока (генератором). Силы, которые разделяют заряды, называют сторонними силами. Они носят неэлектрическое происхождение и действуют только внутри источника. При разделении зарядов сторонние силы создают разность потенциалов между концами цепи.
В том случае, если электрический заряд перемещается по замкнутой цепи, то работа электростатических сил равна нулю. Значит, суммарная работа сил ($A$), которые действуют на заряд равна работе сторонних сил ($A_{st}$). Физическая величина, которая характеризует источник тока - это ЭДС источника (${\mathcal E}$), она определена как:
\[{\mathcal E}=\frac{A}{q}\left(1\right),\]где $q$ -- положительный заряд. Движение заряда идет по замкнутому контуру. ЭДС -- не является силой в буквальном смысле. Единица измерения $\left[{\mathcal E}\right]=В$.
Природа сторонних сил может быть различна, так например, в гальваническом элементе сторонние силы являются результатом электрохимических процессов. В машине постоянного тока такой силой является сила Лоренца.
Основные характеристики тока
Направлением тока условно считают направление движения положительных частиц. Значит, направление тока в металлах имеет противоположное направление по отношению к направлению движения частиц.
Электрический ток характеризуют силой тока. Сила тока ($I$) -- скалярная величина, которая равна производной от заряда ($q$) по времени для тока, который течет через поверхность S:
\[I=\frac{dq}{dt}\left(2\right).\]Ток может быть постоянным и переменным. В том случае, если сила тока и его направление не изменяется во времени, то такой ток называют постоянным и для него выражение для силы тока можно записать в виде:
\[I=\frac{q}{t}\left(3\right),\]где сила тока определена, как заряд, который проходит через поверхность S в единицу времени.
В системе СИ основной единицей измерения силы тока является Ампер (А).
\[1A=\frac{1Кл}{1с}.\]Векторной локальной характеристикой тока является его плотность. Вектор плотности тока ($\overrightarrow{j}$)- характеризует каким образом распределен ток по сечению S. Этот вектор направлен в сторону, в которую движутся положительные заряды. По модулю вектор плотности тока равен:
\[j=\frac{dI}{dS'}\left(4\right),\]где $dS'$ - проекция элементарной поверхности $dS$ на плоскость, которая перпендикулярна вектору плотности тока, $dI$ -- элемент силы тока, который течет через поверхности $dS\ и\ dS'$.
Плотность тока в металле может быть представлена как:
\[\overrightarrow{j}=-n_0q_e\left\langle \overrightarrow{v}\right\rangle \ \left(5\right),\]где $n_0$ -- концентрация электронов проводимости, $q_e=1,6{\cdot 10}^{-19}Кл$ -- заряд электрона, $\left\langle \overrightarrow{v}\right\rangle $ -- средняя скорость упорядоченного движения электронов. При максимальных плотностях токов $\left\langle \overrightarrow{v}\right\rangle ={10}^{-4}\frac{м}{с}$.
Закон сохранения заряда
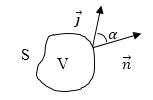
Рис. 1
Фундаментальным физическим законом является закон сохранения электрического заряда. Если выбрать произвольную замкнутую неподвижную поверхность S (рис.1), которая ограничивает объем V, то количество электричества, которое вытекает за секунду из объема V, определяется как $\oint\limits_S{j_ndS.}$ То же количество электричества можно выразить через заряд: $-\frac{\partial q}{\partial t}$, то есть мы имеем:
\[\frac{\partial q}{\partial t}=-\oint\limits_S{j_ndS\left(6\right),}\]где $j_n$ -- проекция вектора плотности тока на направление нормали к элементу поверхности $dS$, при этом:
\[j_n=jcos\alpha \ \left(7\right),\]где $\alpha $ -- угол между направлением нормали к dS и вектором плотности тока. В уравнении (6) употребляется частная производная для того, чтобы подчеркнуть, что поверхность S неподвижна.
Уравнение (6) -- есть закон сохранения заряда в макроскопической электродинамике. В том случае, если ток постоянен во времени, то закон сохранения заряда запишем в виде:
\[\oint\limits_S{j_ndS=0\left(8\right).}\]Задание: Найдите формулу для расчета конвекционного тока, если он возникает в длинном цилиндре (радиус сечения R), который заряжен по поверхности равномерно и равномерно движется со скоростью $v$. Напряженность поля у поверхности цилиндра E. Скорость движение направлена по оси цилиндра.
Решение:
За основу решения задачи примем определение силы тока в виде:
\[I=\frac{dq}{dt}\left(1.1\right).\]Из формулы (1.1) следует, что надо определить элемент заряда, который находится на поверхности цилиндра.
Напряженность поля равномерно заряженного цилиндра на его поверхности может быть найдена по формуле:
\[E=\frac{\sigma }{{\varepsilon }_0}\left(1.2\right),\]где $\sigma $ -- поверхностная плотность заряда, ${\varepsilon }_0=8,85\cdot {10}^{-12}\frac{{Кл}^2}{Н\cdot м^2}.$ Из (1.2) выразим $\sigma $, получим:
\[\sigma =E\cdot {\varepsilon }_0\ \left(1.3\right).\]Поверхностная плотность заряда связана с элементарным зарядом с помощью формулы:
\[\frac{dq}{dS}=\sigma \left(1.4\right).\]Следовательно, из (1.3) и (1.4) получаем:
\[dq=E•е_0dS\left(1.5\right).\]Элемент поверхности цилиндра можно выразить через его параметры как:
\[dS=2\pi \cdot Rdh\left(1.6\right),\]где $dh$- элемент высоты цилиндра. Тогда элемент заряда поверхности цилиндра запишем как:
\[dq=E\cdot {\varepsilon }_0\cdot 2\pi \cdot Rdh\left(1.7\right).\]Подставим полученное выражение (1.7) в (1.1), имеем:
\[I=\frac{d\left(E\cdot {\varepsilon }_0\cdot 2\pi \cdot Rdh\right)}{dt}=2\pi R{\varepsilon }_0E\frac{dh}{dt}\left(1.8\right).\]Так как цилиндр движется вдоль своей оси, то можно записать:
\[\frac{dh}{dt}=v\ \left(1.9\right).\]Получаем в результате:
\[I=2\pi R{\varepsilon }_0Ev.\]Ответ: Конвективный ток $I=2\pi R{\varepsilon }_0Ev.$
Задание: Ток в проводнике изменяется в соответствии с законом: $I=1+3t.$ Какой заряд проходит через поперечное сечение проводника за время t при его изменении от $t_1=3\ с\ \ до\ t_2=7\ с?$ Каким должен быть постоянный ток, чтобы за то же время прошло тот же заряд?
Решение:
За основу решения задачи примем выражение, которое связывает силу тока и заряд, который проходит через поперечное сечение проводника, а именно:
\[I=\frac{dq}{dt}\left(2.1\right).\]Из (2.1) следует, что заряд (количество электричества), который проходит через поперечное сечение проводника за время от$\ t_1\ до{\ t}_2$ можно найти как:
\[q=\int\limits^{t_2}_{t_1}{Idt}\left(2.2\right).\]Подставим, имеющийся в условиях задачи закон изменения тока в уравнение (2.2), получим:
$q=\int\limits^{t_2}_{t_1}{(1+3t)dt}=\int\limits^{t_2}_{t_1}{dt}+\int\limits^{t_2}_{t_1}{3tdt}=\left(t_2-t_1\right)+3\cdot {\left.\frac{t^2}{2}\right|}^{t_2}_{t_1}=\left(t_2-t_1\right)+\frac{3}{2}\left({t_2}^2-{t_1}^2\right)(2.3)$
Вычислим заряд:
\[\ q=\left(7-3\right)+\frac{3}{2}\left(7^2-3^2\right)=4+\frac{3}{2}\cdot 40=64\ \left(Кл\right).\]Для постоянного тока при вычислении силы тока можно использовать формулу:
\[I_{const}=\frac{q}{t}\left(2.3\right),\]где $t$ -- время, за которое через поперечное сечение проводника пройдет заряд q.
В нашем случае время прохождения заряда равно:
\[t=t_2-t_1\left(2.4\right).\]Тогда (2.3) запишем как:
\[I_{const}=\frac{q}{t_2-t_1}\left(2.5\right).\]Можно провести вычисления:
\[I_{const}=\frac{64}{7-3}=\frac{64}{4}=16\ (А)\]Ответ: $q=64Кл\ .$ $I_{const}=16\ A.$












