Определения вихревого поля Отсутствие магнитных зарядов
Линии индукции любого магнитного поля непрерывны, у них нет начала и конца, они либо замкнуты, либо уходят в бесконечность и совершенно не важно, какими контурами с током порождаются эти поля. Векторные поля, которые обладают непрерывными силовыми линиями, называются вихревыми полями. И так, магнитное поле является вихревым.
Электростатические поля имеют силовые линии, которые начинаются и заканчиваются на электрических зарядах, они всегда разомкнуты. Линии магнитного поля, напротив, всегда замкнуты, что означает, что магнитных зарядов в природе не существует.
Движение электрических зарядов образует электрический ток. Так как магнитных зарядов не существует, то не существует и магнитного тока. Отсутствие магнитных зарядов выражает следующее уравнение:
Можно вихревое поле определить иначе.
Векторные поля, вектор которых не равен нулю, называют вихревыми полями.
Исходя из теоремы о циркуляции в локальном виде:
\[rot\overrightarrow{B}={\mu }_0\overrightarrow{j}\ \left(2\right),\](где $\overrightarrow{j}$ -- объемная плотность тока) и второй формы определения вихревого поля можно сделать вывод о том, что магнитное поле является вихревым там, где текут токи и безвихревым, где токов нет.
В том случае, если токов нет, вектор индукции ($\overrightarrow{B}$) можно представить в виде градиента скалярного магнитного потенциала (${\varphi }_m$):
\[\overrightarrow{B}=-grad{\varphi }_m\left(3\right).\]Надо заметить, что при наличии токов такое представление невозможно.
Различие между потенциальными и вихревыми полями
Основными уравнениями магнитного поля постоянных токов являются выражения:
\[\left\{ \begin{array}{c} rot\overrightarrow{B}={\mu }_0\overrightarrow{j}\ , \\ div\overrightarrow{B}=0. \end{array} \right.(4)\]Сравним их с основными уравнениями электростатики:
\[\left\{ \begin{array}{c} rot\overrightarrow{E}=0\ , \\ div\overrightarrow{E}=\frac{1}{{\varepsilon }_0}\rho . \end{array} \right.\left(5\right).\]Из системы уравнений (5) очевидно, что электростатическое поле всегда потенциально, его источниками служат электростатические (неподвижные) заряды. Магнитное поле является вихревым (при наличии токов). Магнитное напряжение зависит от формы контура и не определяется только положением начала и конца этого контура. Однозначной разности потенциалов в магнитном поле не существует. Магнитное напряжение по замкнутому контуру, в общем случае, не равно нулю. Источниками поля служат электрические токи. Магнитное поле называют полем чисто вихревым, в том смысле, что его дивергенция везде равно нулю. Такие поля называют соленоидальным. Потенциальное электростатическое поле полностью определяется, если задана дивергенция напряженности ($div\overrightarrow{E}(x,y,z,)$) как функции координат. Вихревое магнитное поле полностью определяется, когда задана мощность его вихрей, то есть $rot\overrightarrow{B}(x,y,z)$ как функция координат.
Задание: Покажите, почему для вихревого магнитного поля не возможно представить вектор индукции ($\overrightarrow{B}$) в виде градиента магнитного потенциала (${\varphi }_m$).
Решение:
Допустим, что мы можем записать:
\[\overrightarrow{B}=-grad{\varphi }_m\left(1.1\right).\]Применим операцию $rot$ для уравнения (1.1), получим:
\[rot\overrightarrow{B}=-rot(grad{\varphi }_m)\left(1.2\right).\]Известно, что:
\[rot\left(grad{\varphi }_m\right)=0\left(1.3\right).\]Если подставить (1.3) в (1.2) мы видим, что:
\[rot\overrightarrow{B}=0.\]По теореме о циркуляции получается, что токи отсутствуют. Следовательно, представление вектора индукции магнитного поля не возможно в виде магнитного потенциала в области, где текут токи.
Задание: Использовать понятие скалярного магнитного потенциала (${\varphi }_m$) можно только в области пространства, где $\overrightarrow{j}=0.$ Однако и в этой части пространства ${\varphi }_m$ функция не однозначная. Покажите это.
Решение:
Рассмотрим магнитное поле возле контура с током (рис.1). В соответствии с теоремой о циркуляции для любого контура выполняется равенство:
\[\oint\limits_L{\overrightarrow{B}\overrightarrow{dl}=}0\ \left(2.1\right).\]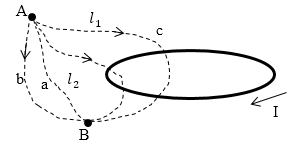
Рис. 1
Так как при отсутствии токов магнитное поле становистя потенциальным, интеграл, который берется между точками A и B не зависит от пути интегрирования, то можно записать:
\[\int\limits_{AaB}{\overrightarrow{B}\overrightarrow{dl}}=\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}\ \left(2.2\right).\]Следовательно:
\[\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}=\int\limits^B_A{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}-{\varphi }_{mB}\left(2.3\right).\]Выражение (2.3) можно рассматривать как разность скалярных магнитных потенциалов в точках A и B. Если поступить, как делалось для потенциала в электростатике, то есть принять, что в какой то точке, например токе B потенциал равне нулю, то запишем:
\[\int\limits^B_A{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}\left(2.4\right).\]Однако, если выбрать контур, который будет охватывать какой-либо ток, например контур AcbB (рис.1) в таком случае линейный интеграл по замкнутому контуру от циркуляции вектора индукции по нему будет отличен от нуля:
\[\oint\limits_{AcbB}{\overrightarrow{B}\overrightarrow{dl}\ne }0\ \left(2.5\right).\]или
\[\oint\limits_{AcBbА}{\overrightarrow{B}\overrightarrow{dl}=\int\limits_{AсB}{\overrightarrow{B}\overrightarrow{dl}}}-\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}=I\ne 0\left(2.6\right).\]В таком случае:
\[\int\limits_{AсB}{\overrightarrow{B}\overrightarrow{dl}}=\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}+I=ц_{mA}-ц_{mB}+I\ \left(2.7\right).\]Так, если мы выберем какой - то путь AnB, который охватывает ток n- раз, то получим:
\[\int\limits_{AnB}{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}-{\varphi }_{mB}+nI(2.8)\]Зададим нулевой потенциал в точке B, тогда имеем, что:
\[\int\limits_{AnB}{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}+nI\left(2.9\right).\]Уравнение (2.9) показывает, что скалярный магнитный потенциал -- не однозначная величина.











