Интегральная форма теоремы о циркуляции
Линии индукции магнитного поля, которое возникает вокруг постоянного тока, который течет по прямолинейному длинному проводнику -- концентрические окружности с центрами на линии тока. Интеграл вида $\oint\limits_L{\overrightarrow{B}d\overrightarrow{l}}\ $- циркуляция вектора $\overrightarrow{B}$ по замкнутому контуру L. Найдем $\oint\limits_L{\overrightarrow{B}d\overrightarrow{l}}$ по некоторому замкнутому контуру вокруг тока I (рис. 1).
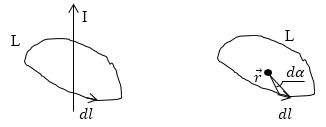
Рис. 1
Линии магнитной индукции лежат в плоскостях перпендикулярных линии тока I, контур L выбираем в плоскости одной из линий $\overrightarrow{B}.$ Используем рис.1, получим:
Обозначим $\left(\widehat{\overrightarrow{B}d\overrightarrow{l}}\right)=\alpha $, тогда имеем:
По условию магнитное поле создает бесконечно длинный прямой проводник с током, индукцию поля которого мы знаем, и запишем в точке на расстоянии r от проводника как:
Подставим (3) и (2) в формулу (1), получим:
Теперь найдем циркуляцию вектора магнитной индукции, используя (4), получим:
где использовано то, что для замкнутого контура, который окружает начало координат:
Из полученного результата в (5) видим, что циркуляция вектора магнитной индукции по замкнутому контуру вокруг тока не зависит от вида контура и определена только силой тока. В том случае если контур ток не охватывает, то циркуляция вектора индукции равна нулю.
Тогда теорема о циркуляции для нескольких токов формулируется следующим образом:
Циркуляция индукции магнитного поля постоянных токов по произвольному замкнутому контуру равна алгебраической сумме токов, которые пронизывают этот контур.
В математическом виде данная формулировка выглядит как уравнение:
\[\oint\limits_L{\overrightarrow{B}d\overrightarrow{l}}=м_0\sum\limits^n_{k=1}{I_k=м_0I\left(7\right),}\]где через I -- обозначают полный ток (алгебраическая сумма всех токов, охватываемых контуром). Теорема о циркуляции еще называется законом полного тока. Надо иметь в виду, что циркуляция вектора $\overrightarrow{B}$ по замкнутому контуру равна нулю не только в случае отсутствия токов, которые пронизывают заданный контур, но и если токи текут в противоположных направлениях и в сумме дают ноль. В формуле (7) знак тока учитывается по правилу правого винта. Этот закон мы получили для прямого бесконечного проводника, но он справедлив и для произвольного тока.
Дифференциальная форма теоремы о циркуляции
Пусть S -- поверхность, которую охватывает контур L. Положительная нормаль к поверхности связана с направлением обхода контура L правилом правого винта. Силу полного тока, который течет через поверхность S можно записать как:
\[I=\int\limits_S{\overrightarrow{j}d\overrightarrow{S}(8)},\]где $\overrightarrow{j}$ -- объёмная плотность тока. В таком случае теорему о циркуляции запишем как:
\[\oint\limits_L{\overrightarrow{B}d\overrightarrow{l}}={\mu }_0\int\limits_S{\overrightarrow{j}d\overrightarrow{S}\left(9\right).}\]По теореме Стокса можно записать, что:
\[\oint\limits_L{\overrightarrow{B}d\overrightarrow{l}}=\int\limits_S{rot\overrightarrow{B}d\overrightarrow{S}}\left(10\right).\]Следовательно, запишем:
\[\int\limits_S{(rot\overrightarrow{B}-{\mu }_0\overrightarrow{j})d\overrightarrow{S}}=0\left(11\right).\]Равенство (11) выполняется для любой поверхности, следовательно, подынтегральное выражение также равно нулю:
\[rot\overrightarrow{B}-{\mu }_0\overrightarrow{j}=0\to rot\overrightarrow{B}={\mu }_0\overrightarrow{j}\ \left(12\right).\]Равенство (12) дифференциальная форма теоремы о циркуляции. Она справедлива для произвольного поля в каждой точке.
Напомним, что теорема о циркуляции в виде (7) и (12) записана для поля в вакууме и стационарных токов.
Задание: Тороид имеет каркас в виде тора и на него намотан проводник, по которому течет ток. Магнитное поле данной конфигурации токов сосредоточено в основном внутри тороида. Поле имеет осевую симметрию. Силовые линии магнитного поля тороида представляют собой окружности с центром на оси тороида. Используя теорему о циркуляции, найдите магнитное поле внутри тороида (рис.2) (B(r)). Если сила тока в нем равна I. N -- число витков тороида.
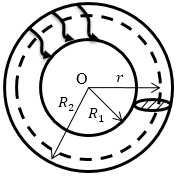
Рис. 2
Решение:
В качестве контура циркуляции выберем силовую линию в виде окружности радиуса r (рис.2). Запишем, что циркуляция вектора индукции магнитного поля вдоль выбранной окружности равна:
\[\oint\limits_L{\overrightarrow{B}d\overrightarrow{l}}=B2\pi r\ \left(1.1\right).\]Тогда теорема о циркуляции предстанет в виде:
\[B2\pi r={\mu }_0NI\left(2.1\right),\]где $N$ -- число витков с током. Выразим модуль вектора индукции, получим:
\[B=\frac{{\mu }_0NI}{2\pi r}.\]Ответ: $B=\frac{{\mu }_0NI}{2\pi r}.$
Задание: Какова циркуляция вектора индукции вдоль контура, который охватывает токи $I_1=5\ A,\ I_2=6\ A$, $I_3=10\ A$, если первые два тока текут в одном направлении, третий в противоположном.
Решение:
По теореме о циркуляции:
\[\oint\limits_L{\overrightarrow{B}d\overrightarrow{l}}=\sum{I_k\left(2.1\right).}\]Для нашего случая имеем:
\[\oint\limits_L{\overrightarrow{B}d\overrightarrow{l}}=I_1+\ I_2-I_3\left(2.2\right).\]Проведем вычисление, получим:
\[\oint\limits_L{\overrightarrow{B}d\overrightarrow{l}}=5+6-10=1\ \left(Тл\cdot м\right).\]Ответ: $\oint\limits_L{\overrightarrow{B}d\overrightarrow{l}}=1Тл•м.$











