Определение силы магнитной силы
Если заряд движется в магнитном поле, то на него действует сила ($\overrightarrow{F}$), которая зависит от величины заряда (q), скорости движения частицы ($\overrightarrow{v}$) относительно магнитного поля, и индукции магнитного поля ($\overrightarrow{B}$). Эта сила была установлена экспериментально, называется она магнитной силой.
И имеет в системе СИ вид:
\[\overrightarrow{F}=q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(1\right).\]Модуль силы в соответствии с (1) равен:
\[F=qvBsin\alpha \ \left(2\right),\]где $\alpha $ -- угол между векторами $\overrightarrow{v\ }и\ \overrightarrow{B}$. Из уравнения (2) следует, что если заряженная частица движется вдоль линии магнитного поля, то не испытывает действия магнитной силы.
Направление магнитной силы
Магнитная сила, исходя из (1) направлена перпендикулярно плоскости, в которой лежат векторы $\overrightarrow{v\ }и\ \overrightarrow{B}$. Ее направление совпадает с направлением векторного произведения $\overrightarrow{v\ }и\ \overrightarrow{B}$ в том случае, если величина движущегося заряда больше нуля, и направлена в противоположную сторону, если $q
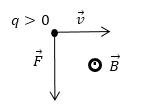
Рис. 1
Свойства силы магнитной силы
Магнитная сила работы над частицей не свершает, так как всегда направлена перпендикулярно скорости ее движения. Из этого утверждения следует, что с помощью воздействия на заряженную частицу с помощью постоянного магнитного поля ее энергию изменить нельзя.
Сила Лоренца
Если на частицу, обладающую зарядом, действуют одновременно электрическое и магнитное поля, то равнодействующая сила может быть записана как:
\[\overrightarrow{F}=q\overrightarrow{E}+q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(3\right).\]Сила, указанная в выражении (3) называется силой Лоренца. Часть $q\overrightarrow{E}$ является силой, действующей со стороны электрического поля на заряд, $q\left[\overrightarrow{v}\overrightarrow{B}\right]$ характеризует силу действия магнитного поля на заряд. Сила Лоренца проявляется при движении электронов и ионов в магнитных полях.
Задание: Протон ($p$) и электрон ($e$), ускоренный одинаковой разностью потенциалов влетают в однородное магнитное поле. Во сколько раз радиус кривизны траектории движения протона $R_p$отличается от радиуса кривизны траектории электрона $R_e$. Углы, под которыми влетают частицы в поле, одинаковы.
Решение:
Если действием силы тяжести в сравнении с действием магнитной силы пренебречь, то второй закон Ньютона запишем как:
\[ma_n=qvBsin\alpha \ \left(1.1\right).\]В формуле (1.1) мы учли, что вектор магнитной составляющей силы Лоренца перпендикулярен скорости и, следовательно, сообщает заряженной частице нормальное ускорение ($a_n$). Его мы можем выразить как:
\[a_n=\frac{v^2}{R}\left(1.2\right).\]По условию задачи заряженные частицы до попадания в магнитное поле ускоряются электрическим полем, для того, чтобы узнать скорость, с которой частицы влетают и движутся в магнитном поле, запишем из закона сохранения энергии:
\[\frac{mv^2}{2}=qU\left(1.3\right).\]Из формулы (1.3) выразим скорость движения частицы:
\[v=\sqrt{\frac{2qU}{m}}\left(1.4\right).\]Подставим (1.2), (1.4) в (1.1), выразим радиус кривизны траектории:
\[m\frac{v}{R}=qBsin\alpha \to R=\frac{mv}{qBsin\alpha }\to R=\frac{\sqrt{2Um}}{B\sqrt{q}sin\alpha }\left(1.5\right).\]Подставим данные для разных частиц, найдем отношение $\frac{R_p}{R_e}$:
\[\frac{R_p}{R_e}=\frac{\sqrt{2Um_p}}{B\sqrt{q_p}sin\alpha }\cdot \frac{B\sqrt{q_e}sin\alpha }{\sqrt{2Um_e}}=\frac{\sqrt{m_p}}{\sqrt{m_e}}.\]Заряды протона и электрона по модулю равны. Масса электрона $m_e=9,1\cdot {10}^{-31}кг,m_p=1,67\cdot {10}^{-27}кг$.
Проведем вычисления:
\[\frac{R_p}{R_e}=\sqrt{\frac{1,67\cdot {10}^{-27}}{9,1\cdot {10}^{-31}}}\approx 42.\]Ответ: Радиус кривизны протона в 42 раза больше, чем радиус кривизны электрона.
Задание: Найдите напряженность электрического поля (E), если протон в скрещенном магнитном и электрическом полях движется прямолинейно. В эти поля он влетел, пройдя ускоряющую разность потенциалов равную U. Поля скрещены под прямым углом. Индукция магнитного поля равна B.
Решение:
На частицу, по условиям задачи действует сила Лоренца, имеющая две составные части: магнитную и электрическую. Первая составляющая магнитная она равна:
\[\overrightarrow{F_m}=q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(2.1\right).\]$\overrightarrow{F_m}$ -- направлена перпендикулярно $\overrightarrow{v\ }и\ \overrightarrow{B}$. Электрическая составляющая силы Лоренца равна:
\[\overrightarrow{F_q}=q\overrightarrow{E}\left(2.2\right).\]Сила $\overrightarrow{F_q}$- направлена по напряженности $\overrightarrow{E}$. Мы помним, что протон имеет положительный заряд. Для того чтобы протон двигался прямолинейно необходимо, чтобы магнитная и электрическая составляющие силы Лоренца уравновешивали друг друга, то есть их геометрическая сумма была равна нулю. Изобразим силы, поля и скорость движения протона, выполнив условия их ориентации на рис. 2.
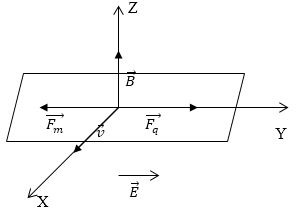
Рис. 2
Из рис.2 и условия равновесия сил запишем:
\[qE-qvB=0\ \left(2.3\right).\]Выразим из (2.3) напряженность электрического поля, получим:
\[E=vB\ \left(2.4\right).\]Скорость найдем из закона сохранения энергии:
\[\frac{mv^2}{2}=qU\to v=\sqrt{\frac{2qU}{m}}\left(2.5\right).\]Подставим (2.5) в (2.4), получим:
\[E=B\sqrt{\frac{2qU}{m}}.\]Ответ: $E=B\sqrt{\frac{2qU}{m}}.$











