Индукция магнитного поля элементарного тока
Напомним, что элементарным замкнутым током называют линейный ток, который обтекает поверхность с бесконечно малыми в физическом смысле линейными размерами.
В разделе «Элементарный ток и его магнитный момент» нами была получена формула для векторного потенциала магнитного поля элементарного тока:
\[\overrightarrow{A}\left(\overrightarrow{r}\right)=\frac{{\mu }_0}{4\pi }\frac{\overrightarrow{p_m}\times \overrightarrow{r}}{r^3}\left(1\right),\]где $\overrightarrow{p_m}$ -- магнитный момент элементарного тока, $\overrightarrow{r}$ -- радиус -- вектор от витка с током до точки, в которой рассматривается поле.
Используя формулу (1) и определение векторного магнитного потенциала(2):
\[\overrightarrow{B}=rot\overrightarrow{A}\ (2)\]применяя операцию rot к формуле (1) получаем формулу, определяющую магнитную индукцию элементарного замкнутого тока:
\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\left\{\frac{3(\overrightarrow{p_m}\cdot \overrightarrow{r})\overrightarrow{r}}{r^5}-\frac{\overrightarrow{p_m}}{r^3}\right\}\left(3\right).\]Элементарный ток в магнитном поле
Теперь выясним, каково поведение элементарного тока, если его поместить во внешнее магнитное поле. Допустим, что поле однородно ($\overrightarrow{B}=const$). Известно, что на подобный контур будет действовать сила Ампера, которая вычисляется в соответствии с одноимённым законом:
\[\overrightarrow{F}=\oint{I\left[\overrightarrow{dl}\overrightarrow{B}\right]}=I\left(\oint{dl}\right)\times \overrightarrow{B}\left(4\right),\]где силу тока и вектор магнитной индукции вследствие их постоянства вынесли за знак интеграла. При этом мы помним, что имеем дело с векторным произведением. Интеграл:
\[\oint{dl}=0\ \left(5\right).\]Формула (5) справедлива для контуров любой формы и при любом расположении контура относительно направления линий поля. Получаем, что в однородном магнитном поле результирующая сила равна нулю ($\overrightarrow{F}=0,\ при\ \overrightarrow{B}=const$).
Вращающий момент ($\overrightarrow{M}$), создаваемый силами, которые приложены к контуру относительно некоторой точки О, в однородном магнитном поле равен:
\[\overrightarrow{M}=\left[\overrightarrow{p_m}\overrightarrow{B}\right](6),\]где $\overrightarrow{p_m}$=I$\overrightarrow{S}=IS\overrightarrow{n}$ -- магнитный момент элементарного контура, $\overrightarrow{n}$ -- положительная нормаль к контуру. Модуль $\overrightarrow{M}$ равен:
\[М=p_mBsin\alpha \ \left(7\right),\]где $\alpha $ -- угол между векторами$\overrightarrow{{\ p}_m}$ и $\overrightarrow{B}$.
Если $\overrightarrow{p_m}\uparrow \uparrow \overrightarrow{B}$ магнитные силы, которые действуют на отдельные участки контура, не пытаются ни повернуть, ни сдвинуть контур. Они пытаются его только растянуть в его плоскости. В случае $\overrightarrow{p_m}\uparrow \downarrow \overrightarrow{B}$ магнитные силы сжимают контур с током.
Если надо увеличить угол между векторами индукции магнитного поля и вектором магнитного момента элементарного тока на $d\alpha \ $надо совершить работу против сил магнитного поля равную:
\[dA=Md\alpha =p_mBsin\alpha \ d\alpha \ \left(8\right).\]Работа (8) идет на увеличении потенциальной энергии $W_{pmeh}$, которую имеет контур с током в магнитном поле:
\[{dW}_{pmeh}=p_mBsin\alpha \ d\alpha \ \left(9\right).\]Найдем интеграл от (9), получим:
\[W_{pmeh}={-p}_mBcos\alpha +const\left(10\right).\]Допустим, что в (10) $const$=0, в таком случае имеем:
\[W_{pmeh}={-p}_mBcos\alpha ={-\overrightarrow{p}}_m\overrightarrow{B}\left(11\right).\]Если векторы ${\overrightarrow{p}}_m\ и\ \overrightarrow{B}$ ориентированы параллельно, то мы имеем минимум потенциальной энергии, то есть положение устойчивого равновесия. Величина $W_{pmeh}$- это не полная потенциальная энергия контура с током, а только та ее часть, которая обусловлена вращательным моментом.
Задание: Найдите работу (А), которую необходимо совершить внешним силам для того, чтобы повернуть контур с током относительно его оси, которая проходит через середину его противоположных сторон на угол $\frac{\pi }{2}$. Если по контуру течет постоянный ток I, контур свободно установился в магнитном поле с индукцией B. Сторона квадрата равна $a$.
Решение:
Механический момент, который действует на контур можно вычислить в соответствии с формулой:
\[М=p_mBsin\alpha \ \left(1.1\right),\]где $\alpha $ -- угол между векторами$\overrightarrow{{\ p}_m}$ и $\overrightarrow{B}$. По условию задачи контур с заданной силой тока находится в равновесии в поле с индукцией B. Это означает, что момент сил, которые действуют на контур, равен нулю, то есть $\overrightarrow{{\ p}_m}$ $\uparrow \uparrow $ $\overrightarrow{B}$, $\alpha =0.$
Если к контуру приложить внешнюю силу, то ее работа по повороту контура на угол $d\alpha $ будет равна:
\[dA=Md\alpha \ \left(1.2\right).\]Подставим в (1.2) выражение (1.1), учтем, что $p_m=IS=Ia^2$ получим:
\[dA=Ia^2Bsin\alpha d\alpha \ \left(1.3\right).\]Возьмем интеграл от выражения (1.3), где $0\le \alpha \le \frac{\pi }{2}$, получим:
$А=\int\limits^{\frac{\pi }{2}}_0{Ia^2Bsin\alpha d\alpha }=Ia^2B\int\limits^{\frac{\pi }{2}}_0{sin\alpha d\alpha }=Ia^2B.$
Ответ: $А=Ia^2B.$
Задание:
Система состоит из двух одинаковых контуров с током (рис.1). Магнитные моменты этих контуров равны ${\ p}_m\ $ и они взаимно перпендикулярны. Чему равен механический момент, который действует на контур (2), если расстояние между контурами равно d, контуры можно считать элементарными токами.
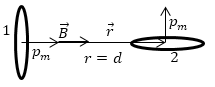
Рис. 1
Решение:
Элементарный ток (1) создает магнитное поле, индукцию которого можно найти как:
\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\left\{\frac{3(\overrightarrow{p_m}\cdot \overrightarrow{r})\overrightarrow{r}}{r^5}-\frac{\overrightarrow{p_m}}{r^3}\right\}\left(2.1\right).\]Учтем, что расстояние между контурами равно d, и угол между векторами $\overrightarrow{p_m}$ и $\overrightarrow{r}$ равен нулю. Тогда выражение (2.1) преобразуется к виду, запишем его по модулю:
\[В=\frac{{\mu }_0}{4\pi }\left(\frac{3p_m}{d^3}-\frac{p_m}{d^3}\right)=\frac{{\mu }_0p_m}{2\pi d^3}\left(2.2\right).\]Механический момент, который действует на элементарный ток с номером (2) можно вычислить по формуле:
\[М=p_mBsin\alpha \ \left(2.3\right),\]где угол $\alpha $=$\frac{\pi }{2}$, тогда подставим в (2.3) выражение для B из (2.2), получим:
\[М=p_m\frac{{\mu }_0p_m}{2\pi d^3}=\frac{{\mu }_0{p_m}^2}{2\pi d^3}.\]Ответ: $М=\frac{{\mu }_0{p_m}^2}{2\pi d^3}.$











