Математическая запись отсутствия магнитных зарядов
На ранних стадиях изучения магнитных явлений предполагалось, что источниками магнитных полей являются магнитные заряды, которые взаимодействуют по закону Кулона. Однако такое предположение не согласуется с одним из основных уравнений магнитостатики:
Или в интегральном виде:
Электрические токи - источники магнитных полей
Сам Кулон еще отмечал на принципиальное различие между электрическими и магнитными явлениями. Оно, прежде всего в том, что ни как не можем разделить в теле серверный и южный полюса магнита, чтобы получить тело только с одним магнитным полюсом. И мы не можем получить тела с избытком того или иного магнетизма (северного или южного). Из этой ситуации Кулон сделал вывод о том, что два вида магнитных зарядов неразрывны. Дальнейшее изучение магнитных явлений показало, что гипотеза существования магнитных зарядов неверна в корне. Магнитных зарядов не существует. Каждый атом вещества надо рассматривать как круговой ток. Магнитное поле намагниченного тела складывается из магнитных полей кругового тока.
Доказательство того, что магнитный поток вектора магнитной индукции через замкнутую поверхность равен нулю
Формулы (1) и (2) показывают, что магнитных зарядов не существует. Докажем, что магнитный поток $\oint{\overrightarrow{B}d\overrightarrow{S}}$ через любую замкнутую поверхность S равен нулю (2).
Предположим, что магнитное поле создают точечные заряды (q), которые равномерно движутся. Тогда индукцию магнитного поля ($\overrightarrow{B_q}$) таких зарядов модно представить как:
где $\overrightarrow{v}$ -- скорость движения заряженной частицы, $\overrightarrow{r}$ -- радиус -- вектор, который проводится из заряда, в рассматриваемую току поля, $\left [\overrightarrow{v}\overrightarrow{r}\right]\ $- векторное произведение соотвествующих векторов. Так как для магнитных полей движущихся зарядов выполняется принцип суперпозиции. Поток векторной суммы нескольких векторов через любую поверхность равен алгебраической сумме потоков отдельных векторов через ту же поверхность. Значит, мы при доказательстве можем ограничиться рассмотрением одной движущейся частицей. Пусть заряд движется с постоянной скоростью перпендикулярно плоскости рис.1.
Магнитные силовые линии при этом -- коаксиальные окружности. Их плоскости параллельны плоскости рис.1, а центры расположены на прямой, по которой движется заряд. Рассмотрим бесконечно тонкую кольцевую трубку, которую образуют магнитные силовые линии (АВСД). Из-за осевой симметрии магнитный поток через поперечное сечение этой трубки постоянный на всей ее длине. Трубка пересекает замкнутую поверхность S четное число раз. Магнитные потоки через площадки $dS_1и\ dS_2$, которые вырезаны трубкой на поверхности S, одинаковы по модулю, противоположны по знаку. В результате сумма таких потоков равна нулю. Все пространство можно разбить на подобные тонкие кольцевые магнитные трубки.
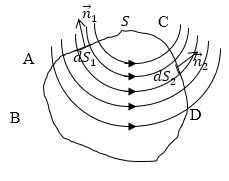
Рис. 1
Так, суммарный магнитный поток через замкнутую поверхность S равен нулю. Мы доказали, что:
Уравнение (2) и эквивалентное ему уравнение (1) в дифференциальном виде:
справедливы для любых магнитных полей.
Силовые поля, дивергенции которых везде равны нулю, называются соленоидальными полями.
Источником магнитного поля являются не магнитные заряды, а электрические токи.
Задание: Найдите модуль вектора магнитной индукции поля, которое создано двумя длинными прямолинейными проводниками с токами $I_1\ и\ $ $I_2$, которые текут в одном направлении. Расстояние между проводами равно d. Точка, в которой надо найти поле, находится на расстоянии r=d от каждого из проводников.
Решение:
На рис.2 проводники с токами перпендикулярны плоскости рисунка, причем текут от нас.
Силовые линии магнитного поля представляют собой окружности с центрами на проводнике с током.
Векторы магнитной индукции являются касательными к этим окружностям в точке, где мы ищем поле.
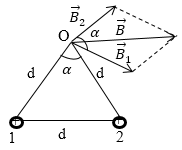
Рис. 2
Таких вектора у нас два (${\overrightarrow{B}}_1и\ {\overrightarrow{B}}_2$). Результирующий вектор будет найден как:
\[{\overrightarrow{В}=\overrightarrow{B}}_1+\ {\overrightarrow{B}}_2\left(1.1\right).\]По теореме косинусов модуль вектора $\overrightarrow{В}$ равен:
\[B=\sqrt{{B_1}^2+{B_2}^2+2B_1B_2cos\alpha }\left(1.2\right).\]Так как треугольник на рис.2 равносторонний, то $\alpha =\frac{\pi }{3}.$ Модуль вектора магнитной индукции поля, которое создает бесконечно длинный проводник с током (для проводника 1) в вакууме в точке О равно:
\[B_1=\frac{{\mu }_0I_1}{2\pi d}\left(1.3\right),\]для проводника (2):
\[B_2=\frac{{\mu }_0I_2}{2\pi d}\left(1.4\right).\]Подставим (1.3) и (1.4) в (1.2) найдем искомое поле, учтем, что $cos\alpha =cos\frac{\pi }{3}=\frac{1}{2}$:
\[B=\frac{{\mu }_0}{2\pi d}\sqrt{{I_1}^2+{I_2}^2+I_1I_2.}\]Ответ: $B=\frac{{\mu }_0}{2\pi d}\sqrt{{I_1}^2+{I_2}^2+I_1I_2.}$
Задание: Найдите магнитную индукцию поля, которое создает электрон, двигаясь по круговой орбите, если ее радиус в атоме водорода равен r.
Решение:
Для решения задачи воспользуемся формулой для определения вектора магнитной индукции, если поле создает движущийся заряд, а именно:
\[\overrightarrow{B_q}=\frac{{\mu }_0}{4\pi }q\frac{\left[\overrightarrow{v}\overrightarrow{r}\right]}{r^3}\left(2.1\right),\]где $\widehat{\overrightarrow{v}\overrightarrow{r}}=\frac{\pi }{2}$ так как из условия электрон движется по окружности, вектор скорости направлен по касательной к окружности, радиус вектор $\overrightarrow{r}$ -- проведен в точку касания. Заряд электрона величина известная и он равен $q=1,6\cdot {10}^{-19}Кл$. Тогда вектор магнитной индукции запишем как:
\[B=\frac{{\mu }_0}{4\pi }\frac{qv}{r^2}\left(2.2\right).\]В соответствии со вторым законом Ньютона на электрон действует кулоновская сила притяжения к ядру атома водорода и она равна:
\[ma=k\frac{q^2}{r^2}\to m\frac{v^2}{r}=k\frac{q^2}{r^2}\ \left(2.3\right),\]где $k=\frac{1}{4\pi {\varepsilon }_0}$, m -- масса электрона.
Выразим из (2.3) скорость движения электрона по своей орбите, получим:
\[v=\sqrt{\frac{q^2}{4\pi {\varepsilon }_0rm}}\left(2.4\right).\]Подставим (2.4) в (2.2), получим:
\[B=\frac{{\mu }_0}{8\pi }\frac{q^2}{r^2\sqrt{\pi {\varepsilon }_0rm}}\ .\]Ответ: $B=\frac{{\mu }_0}{8\pi }\frac{q^2}{r^2\sqrt{\pi {\varepsilon }_0rm}}\ .$ Магнитные поля создаются движущимися зарядами.











