Модуль вектора индукции поля движущегося заряда
Любой движущийся заряд создает вокруг себя магнитное поле. Будем считать, что скорость движения заряда много меньше скорости света. Найдем формулу для расчета такого магнитной индукции такого поля ($\overrightarrow{B}$). Для этого рассмотрим небольшой отрезок проводника (длиной $l$) с током (I). Такой проводник создает в некоторой точке поле, модуль которого можно записать как:
где $r$ -- расстояние от данного проводника, до точки, где ищем поле. Силу тока можно записать через плотность тока (j) как:
а плотность тока через концентрацию заряженных частиц:
где $n$ - концентрация частиц, $q$ - заряд частиц, $v$ -- модуль скорости их движения. Тогда произведение силы тока на длину проводника можно выразить как:
где $N$ -- суммарное число зарядов на отрезке проводника. Подставляя в (1) получим для вектора индукции:
Значит индукция поля, которое создает одна заряженная частица, равна:
Направление вектора индукции поля движущегося заряда
Направление вектора индукции магнитного поля, создаваемого одной частицей перпендикулярно к вектору скорости ($\overrightarrow{v}$) частицы и радиус- вектору ($\overrightarrow{r}$), который проведен из частицы в рассматриваемую точку и подчиняется правилу правого буравчика. Силовыми линиями поля точечного заряда являются концентрические окружности рис.1.
Значит окончательно, вектор магнитной индукции поля, которое создается движущимся зарядом в системе СИ, можно записать как:
Формула (6) показывает индукцию магнитного поля движущегося положительного заряда. Если мы имеем дело с отрицательным зарядом, то q заменим на --q. Из формулы (6) очевидно, что движущийся заряд эквивалентен элементу тока, то есть:
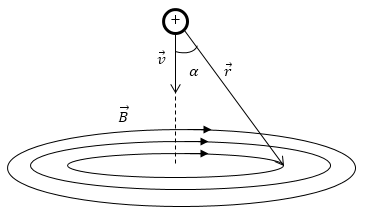
Рис. 1
Влияние магнитного поля на электрическое поле при движении заряда
Необходимо отметить, что появление в формуле для вектора магнитной индукции вектора скорости означает, что в пространстве появляется выделенное направление. Электрическое поле заряда утрачивает свою сферическую симметрию и становится осесимметричным (рис.2). При скорости движения заряда много меньшей чем скорость света в любой момент времени электрическое поле считается не отличающимся от электростатического поля. Но надо помнить, что поле перемещается вместе с зарядом. Поэтому поле изменяется в каждой точке пространства со временем.
При скоростях сравнимых со скоростью света, поле «сплющивается» в направлении движения и сосредоточено около плоскости, которая перпендикулярна вектору скорости ($\overrightarrow{v}$) (рис.2).
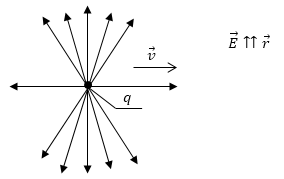
Рис. 2
Задание: Определите магнитную индукцию (В) поля, которое создает электрон, двигаясь прямолинейно с постоянной скоростью, равной 200 $\frac{м}{с}$, в точке на расстоянии r=2$\cdot {10}^{-9}м$ от него, лежащей на прямой, которая проходит через мгновенное положение электрона и составляет угол 450 с вектором скорости.
Решение:
Считаем, что электрон находится в вакууме. За основу решения примем формулу:
\[\overrightarrow{B}=\frac{{\mu }_0q\left[\overrightarrow{v}\overrightarrow{r}\right]\ }{4\pi r^3}\left(1.1\right).\]Модуль вектора магнитной индукции при этом имеет вид:
\[B=\frac{{\mu }_0qvsin\alpha \ }{4\pi r^2}\left(1.2\right),\]где $\alpha $ -- угол между векторами $\overrightarrow{v}\ и\ \overrightarrow{r}.$
Заряд электрона известен $q=1,6\cdot {10}^{-19}Кл,\ {\mu }_0=4\pi \cdot {10}^{-7}\frac{Гн}{м}.$ Проведем расчет:
\[B=\frac{4\pi \cdot {10}^{-7}1,6\cdot {10}^{-19}\cdot 200sin(45{}^\circ )\ }{4\pi {(2\cdot 10^{-9})}^2}=\frac{3,2\cdot {10}^{-24}\cdot \sqrt{2}}{8\cdot {10}^{-18}}=0,56\cdot {10}^{-6}\left(Тл\right).\]Ответ: $B=0,56\ мк\ Тл.$
Задание: Найдите индукцию магнитного поля в центре непроводящей сферы, если по ее поверхности равномерно распределен заряд, плотность которого равна $\sigma .$ Сфера вращается с постоянной угловой скоростью равной $w$ вокруг своей оси.
Решение:
Выделим произвольный бесконечно тонкий слой сферы высоты dx. Произвольную площадку поверхности сферы обозначим как dS. Тогда заряд, который находится на такой площадке, равен:
\[dq=dS\cdot \sigma \ \left(2.1\right).\]Этот заряд, двигаясь вместе с поверхностью сферы, создает магнитное поле в ее центре, которое можно записать как:
\[dB=\frac{{\mu }_0}{4\pi }\frac{dq\cdot v\cdot R}{R^3}=\frac{{\mu }_0}{4\pi }\frac{dS\cdot \sigma \ \cdot w\cdot r}{R^2}\left(2.2\right),\]где $v=w\cdot r,$ где $r$ -- радиус вращения слоя вокруг оси сферы. Весь слой будет создавать индукцию магнитного поля равную:
\[B=\int{\frac{{\mu }_0}{4\pi }\frac{dS\cdot \sigma \ \cdot w\cdot r}{R^2}=}\frac{{\mu }_0}{4\pi }\frac{2\pi r\triangle x\cdot \sigma \ \cdot w\cdot r}{R^2}\left(2.3\right),\]где $\int{dS}=2\pi r\triangle x.$
Сферу можно разделить на бесконечное количество слоев. Каждый слой создает магнитное поле В, которое рассчитывается по формуле (2.3), для нахождения суммарного поля охарактеризуем положение слоя как:
\[r=\sqrt{R^2-x^2}\left(2.4\right),\]где x -- координата по оси Х считая от начала координат, которое мы поместили в центр сферы. $\triangle x=dx$ В таком случае суммарное поле найдется как непрерывная сумма полей слоев, то есть:
\[B_S=\int\limits^R_{-R}{Bdx}=\int\limits^R_{-R}{\frac{{\mu }_0}{4\pi }\frac{2\pi r^2\cdot \sigma \ \cdot w}{R^2}dx}=\int\limits^R_{-R}{\frac{\left(R^2-x^2\right)}{R^2}dx}=\frac{{\mu }_0}{2}\cdot \sigma \ \cdot w\cdot \frac{4R}{3}=\frac{2}{3}{\mu }_0\cdot \sigma \ \cdot w\cdot R.\]Ответ: $B_S=\frac{2}{3}\mu_0•у\ •w•R.$











