Допустим, что в цепи рис.1 действует переменная ЭДС. Она изменяется по закону:
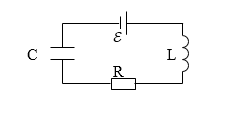
Рисунок 1.
В цепи течет ток вида:
Амплитуда силы тока${\ (I}_m)$ связана с амплитудой ${{\mathcal E}}_m$ «законом Ома» для переменного тока:
Выражение:
полное электросопротивление. Угол ($\varphi $) на который колебания тока отстают от колебаний напряжения определен выражением:
Если изменить частоту колебаний ($\omega $). Как следует из формул (3) , (5) произойдёт изменение амплитуды силы тока ($I_m$) и сдвига фаз ($\varphi $).
Если $\omega =0$, то выражение $\frac{1}{\omega C}\to \infty $. Импеданс ($Z$) становится бесконечным, следовательно, $I_m=0.$ При $\omega =0$ мы имеем дело с постоянным током, который не проходит через конденсатор. Если начать увеличивать частоту, то величина реактивного сопротивления (${\left(\omega L-\frac{1}{\omega C}\right)}^2$) сначала уменьшается, следовательно, уменьшается импеданс, увеличивается $I_m.$ Когда частота ($\omega $) становится равной резонансной частоте контура (${\omega }_0$):
полное сопротивление цепи ($Z$) становится минимальным и равным активному сопротивлению цепи ($R$). Сила тока при этом достигает максимума. При $\omega >{\omega }_0$ выражение ${\left(\omega L-\frac{1}{\omega C}\right)}^2\ne 0$ и растет при росте частоты. Импеданс вновь увеличивается, амплитуда силы тока уменьшается, приближаясь к нулю асимптотически.
Графически вышеописанный процесс изображен на рис.2.
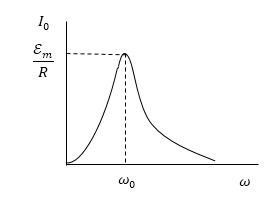
Рисунок 2.
Амплитуда силы тока при резонансной частоте ($\omega ={\omega }_0$) равна:
при этом разность фаз равна нулю ($\varphi =0$). В цепи как бы нет емкости и индуктивности. При этой частоте напряжения на емкости и индуктивности полностью взаимно компенсируются, становясь равными по модулю, так как они по фазе противоположны всегда. Такой резонанс называют резонансом напряжений. Векторная схема резонанса напряжений изображена на рис.3. При резонансе контур ведет себя как активное сопротивление.
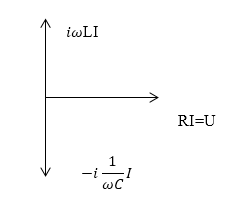
Рисунок 3.
Итак, случай вынужденных колебаний, когда частота генератора ЭДС (или приложенного внешнего напряжения) равна резонансной частоте, представляет особый интерес. При этом амплитуда тока достигает максимума, а сдвиг фаз между током и напряжением равен нулю. Контур действует как активное сопротивление.
Применение резонанса напряжений
Явление резонанса напряжений используют в радиотехнике, если необходимо усилить колебания напряжения какой либо частоты, например в устройствах входной части радиоприемника. В этой части есть колебательный контур ($LC$). Добротность этого контура высока, напряжение с конденсатора контура подается на вход усилителя. Входные сигналы вызывают в антенне переменный ток довольно высокой частоты, который вызывает в катушке $L$ ЭДС взаимной индукции, амплитуда которой ${{\mathcal E}}_m\ \ $. Из-за резонанса на конденсаторе (значит и на входе) появляется напряжение с амплитудой ${{\mathcal E}}_mO>{{\mathcal E}}_m.$ Это усиление работает только в узком интервале частот, около резонансной частоты, что позволит выделить из большого количества сигналов разных радиостанций только колебания нужной частоты.
Задание: Чему равна амплитуда напряжения на конденсаторе ($U_{mC}$) при резонансе напряжений, если колебания затухают слабо? Добротность контура равна$\ O$. Внешняя ЭДС изменяется в соответствии с законом: ${\mathcal E}={{\mathcal E}}_m{sin \left(\omega t\right)\ }.$
Решение:
Амплитуда тока при резонансе достигает максимума, она равна:
\[I_{m\ }\left({\omega }_0\right)=\frac{{{\mathcal E}}_m}{R}\left(1.1\right),\]где ${\omega }_0$ -- резонансная частота.
Следовательно, амплитуда напряжения на конденсаторе будет равна:
\[U_{mC}=X_CI_{m\ }\left(1.2\right),\]где емкостное сопротивление равно:
\[X_C=\frac{1}{\omega_0С}\left(1.3\right).\]Подставим в формулу (1.2) $X_C$ из (1.3) и $I_{m\ }$ из (1.1) получим амплитуду напряжения на конденсаторе при резонансе:
\[U_{mC}=\frac{{{\mathcal E}}_m}{{\omega }_0RС}(1.4).\]Учтем, что:
\[{\omega }_0=\frac{1}{\sqrt{LC}}(1.5)\]подставим выражение для резонансной частоты в формулу (1.4), получим:
\[U_{mC}=\frac{{{\mathcal E}}_m\sqrt{LC}}{RС}={{\mathcal E}}_m\frac{1}{R}\sqrt{\frac{L}{C}}={{\mathcal E}}_mO\ \left(1.6\right),\]где $O=\frac{1}{R}\sqrt{\frac{L}{C}}$ -- добротность контура.
Ответ: $U_{mC}={{\mathcal E}}_mO.$
Задание: Чему равна амплитуда напряжения на индуктивности ($U_{mL}$) при резонансе напряжений, если колебания затухают слабо? Добротность контура равна$\ O$. Внешняя ЭДС изменяется в соответствии с законом: ${\mathcal E}={{\mathcal E}}_m{sin \left(\omega t\right)\ }.$
Решение:
Выражение для напряжения на индуктивности можно записать как:
\[U_{mL}=I_m{\omega }_0L\ \left(2.1\right),\]где выражение для амплитуды тока ($I_m(\omega_0)$) при резонансе напряжений:
\[I_{m\ }\left({\omega }_0\right)=\frac{{{\mathcal E}}_m}{R}\left(2.2\right).\]Получим:
\[U_{mL}=\frac{{{\mathcal E}}_m}{R}{\omega }_0L\ \left(2.3\right).\]Проведем замену:
\[{\omega }_0=\frac{1}{\sqrt{LC}}\left(2.4\right).\]Получим, что амплитуда напряжения на индуктивности равна:
\[U_{mL}=\frac{{{\mathcal E}}_m}{R}\frac{1}{\sqrt{LC}}L=\frac{{{\mathcal E}}_m}{R}\frac{\sqrt{L}}{\sqrt{C}}{={\mathcal E}}_mO.\]Ответ: $U_{mL}{={\mathcal E}}_mO.$
Колебания напряжения на конденсаторе и индуктивности имеют равные амплитуды, но их разность фаз равна $\pi $.











